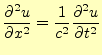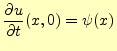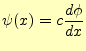このあたりの説明は,参考文献 [1]を大いに参考にした.これは分
かりやすい教科書なので,読んでみると良いだろう.
1次元波動方程式を数値計で解くことを考える.その前に,解くべき方程式と条件をきち
んと書いておく.解くべき方程式と条件は,
となる.弦を伝わる波の速度は1,弦の長さも1としている.この最初の式は波動方程式で
あるが,2番目を初期条件,3番目を境界条件と言う.2番目の初期条件は,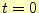 の時の弦
の状態を示しており,
の時の弦
の状態を示しており,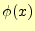 はそのときの弦の形(変位),
はそのときの弦の形(変位),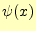 は弦の変位の速度で
ある.
は弦の変位の速度で
ある.
波動方程式を解くためには,初期条件と境界条件が必要である.ある時刻の力学的状態は,
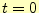 の時の変位と速度が決まり,それ以降の状態が一意に決まる;これは初期条件を表
している.弦の振動の場合は,その境界条件も決める必要がある.これらと波動方程式に
より,それ以降の弦の状態--ある時刻の変位の値--を決ることができ
る.図2に初期条件と境界条件の様子を示す.
の時の変位と速度が決まり,それ以降の状態が一意に決まる;これは初期条件を表
している.弦の振動の場合は,その境界条件も決める必要がある.これらと波動方程式に
より,それ以降の弦の状態--ある時刻の変位の値--を決ることができ
る.図2に初期条件と境界条件の様子を示す.
図 2:
時刻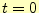 のときの弦の様子(スナップショット).初期条件と境界
条件が表されており,y方向の速度が
のときの弦の様子(スナップショット).初期条件と境界
条件が表されており,y方向の速度が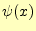 になっている.
になっている.
|
|
まずは,波動方程式を差分方程式に書き直すことからはじめる.これも,いつものように,
解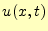 をテイラー展開する.x方向の微小変位を
をテイラー展開する.x方向の微小変位を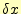 ,時間軸方向の微小変位
を
,時間軸方向の微小変位
を とする.すると,
とする.すると,
となる.これらの式の辺々を足し合わせえると,
が得られる.このことから,2階の偏導関数の値は微小変位 の場所の関数の
値を用いて,
の場所の関数の
値を用いて,
 の精度で近似計算ができることが分かる.すなわち,式(
6)の右辺の第1項を計算すればよいのである.ラプラス
方程式と同じである.同様なことを時間軸方向についても行うと
の精度で近似計算ができることが分かる.すなわち,式(
6)の右辺の第1項を計算すればよいのである.ラプラス
方程式と同じである.同様なことを時間軸方向についても行うと
が得られる.
これらの式(6)と(7)を元の波動
方程式(4)に代入すれば,
となる.これが,1次元波動方程式の差分の式である.この式を計算し易いように,もう
少し変形すると,
とすることができる.この式の右辺は,時刻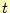 と
と
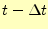 の値である.そして,
左辺は時刻
の値である.そして,
左辺は時刻
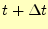 の値である.このことから,式(9)を用いると,時
刻
の値である.このことから,式(9)を用いると,時
刻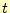 と
と
 の値から,
の値から,
 の値が計算できることになる.
の値が計算できることになる.
実際に式(9)を数値計算する場合,x方向には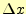 ,時間軸方向には
,時間軸方向には
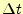 毎に分割する.ラプラス方程式を格子点で分割したのと同じである.格子点に
分割し数値計算する場合,
毎に分割する.ラプラス方程式を格子点で分割したのと同じである.格子点に
分割し数値計算する場合, や
や
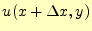 と表現するよりは,
と表現するよりは,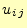 と表現したほうが便利である.そこで,
と表現したほうが便利である.そこで,
と表現を改める.このようにすると,式(9)は
となり,数値計算し易い形になる.ただし,
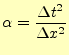 |
(12) |
である.
この式を用いた計算の様子を図3に示す.
波動方程式というけったいな偏微分方程式が,ただ単に数値を順番に代入していく式に変
換されたわけである.この計算は非常に簡単である.ただ,時間領域を1000分割
(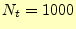 ),x軸領域も1000分割(
),x軸領域も1000分割( )すると,100万回の計算が必要であるが,
コンピューターにとって,その程度の計算は大したことはない.
)すると,100万回の計算が必要であるが,
コンピューターにとって,その程度の計算は大したことはない.
式(11)を計算すると,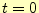 の状態から,時間の経過によって弦の様子が
どうなるか分かる.以下のように,芋づる式に,弦の変位が計算できるわけである.
の状態から,時間の経過によって弦の様子が
どうなるか分かる.以下のように,芋づる式に,弦の変位が計算できるわけである.
このように,計算を盲目的に進めれば,弦の振動の式(4)
の数値計算の結果である近似解が得られる.当然,境界条件
 |
(13) |
を,忘れてはならない.
これを計算するためには,まず,
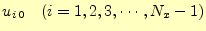 の値を決める
必要がある.これ以前の状態が分からないので,式(11)は使えないが,式
(4)の初期条件が使える.すなわち,
の値を決める
必要がある.これ以前の状態が分からないので,式(11)は使えないが,式
(4)の初期条件が使える.すなわち,
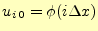 |
(14) |
である.
次に,
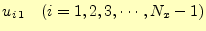 を計算するわけであるが,まだ,式
(11)は使えない.なぜならば,この式は2つ前の状態まで必要なので,こ
れまでのところ,一つ前の状態しか分かっていないからである.そこで,2番目の初期条
件(変位の速度)を使うことになる.計算したい量は
を計算するわけであるが,まだ,式
(11)は使えない.なぜならば,この式は2つ前の状態まで必要なので,こ
れまでのところ,一つ前の状態しか分かっていないからである.そこで,2番目の初期条
件(変位の速度)を使うことになる.計算したい量は
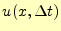 なので,とりあえず
テーラー展開してみる.これを,
なので,とりあえず
テーラー展開してみる.これを,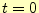 の周りでテーラー展開すると,
の周りでテーラー展開すると,
となる.この右辺の第1と2項は簡単に計算できる.問題は第3項であるが,これは見覚え
のある式である.式(6)と同じである.これを代入すると,
となる.これは,めでたい式である.右辺は, のみの値で構成されている.これで,
のみの値で構成されている.これで,
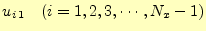 が計算可能になった.この式から,
が計算可能になった.この式から,
![$\displaystyle u_{i\,1}=u_{i\,0} +\psi(x_i)\Delta t +\frac{\alpha}{2}\left[ u_{i+1\,0}-2u_{i\,0}+u_{i-1\,0}\right]$](img64.png) |
(17) |
が得られる.
以上より,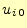 と
と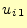 が得られたわけである.
が得られたわけである.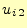 以降は,
式(11)に従い,計算すればよい.
以降は,
式(11)に従い,計算すればよい.
今までの議論で定在波の取り扱いは可能であろう.そこで,進行波の記述方法について,
コメントしておく.進行波を数値計算すると面白いのでその方法を示す.進行波を記述す
るためには,初期条件さえ記述すれば,後の差分方程式は同じである.その初期条件の記
述の仕方を示す.
元の波動方程式
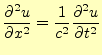 |
(18) |
には,明らかに,ダランベールの解
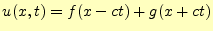 |
(19) |
というものがある.これは元の波動方程式に代入すれば,それを満足していることは直ち
に理解できる.ここで,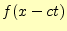 はx軸を正の方向に進む進行波(forward wave)で,
はx軸を正の方向に進む進行波(forward wave)で,
 は負の方向に進む後進波(backward wave)である.
は負の方向に進む後進波(backward wave)である.
初期条件
の波がx軸を正の方向に進む進行波として取り扱うには,どうしたらよいだろうか?.のこ
る条件は,
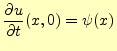 |
(21) |
である.進行波になるように,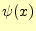 を決めればよい.
を決めればよい.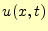 を進行波と仮定する
と,式(20)から
を進行波と仮定する
と,式(20)から
となる.この式を使って, を求めることにする.
を求めることにする.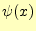 の定義より,
の定義より,
となる.進行波にするためには,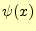 は
は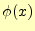 の導関数ににすればよいのである.
の導関数ににすればよいのである.
念のため言っておくが,後進波にするためには
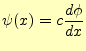 |
(24) |
とすればよい.
ホームページ: Yamamoto's laboratory
著者: 山本昌志
Yamamoto Masashi
平成20年1月31日
![]() の時の変位と速度が決まり,それ以降の状態が一意に決まる;これは初期条件を表
している.弦の振動の場合は,その境界条件も決める必要がある.これらと波動方程式に
より,それ以降の弦の状態--ある時刻の変位の値--を決ることができ
る.図2に初期条件と境界条件の様子を示す.
の時の変位と速度が決まり,それ以降の状態が一意に決まる;これは初期条件を表
している.弦の振動の場合は,その境界条件も決める必要がある.これらと波動方程式に
より,それ以降の弦の状態--ある時刻の変位の値--を決ることができ
る.図2に初期条件と境界条件の様子を示す.
![]() をテイラー展開する.x方向の微小変位を
をテイラー展開する.x方向の微小変位を![]() ,時間軸方向の微小変位
を
,時間軸方向の微小変位
を![]() とする.すると,
とする.すると,

![]() ,時間軸方向には
,時間軸方向には
![]() 毎に分割する.ラプラス方程式を格子点で分割したのと同じである.格子点に
分割し数値計算する場合,
毎に分割する.ラプラス方程式を格子点で分割したのと同じである.格子点に
分割し数値計算する場合,![]() や
や
![]() と表現するよりは,
と表現するよりは,![]() と表現したほうが便利である.そこで,
と表現したほうが便利である.そこで,
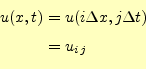
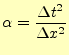
![]() ),x軸領域も1000分割(
),x軸領域も1000分割(![]() )すると,100万回の計算が必要であるが,
コンピューターにとって,その程度の計算は大したことはない.
)すると,100万回の計算が必要であるが,
コンピューターにとって,その程度の計算は大したことはない.

![]() の値を決める
必要がある.これ以前の状態が分からないので,式(11)は使えないが,式
(4)の初期条件が使える.すなわち,
の値を決める
必要がある.これ以前の状態が分からないので,式(11)は使えないが,式
(4)の初期条件が使える.すなわち,
![]() を計算するわけであるが,まだ,式
(11)は使えない.なぜならば,この式は2つ前の状態まで必要なので,こ
れまでのところ,一つ前の状態しか分かっていないからである.そこで,2番目の初期条
件(変位の速度)を使うことになる.計算したい量は
を計算するわけであるが,まだ,式
(11)は使えない.なぜならば,この式は2つ前の状態まで必要なので,こ
れまでのところ,一つ前の状態しか分かっていないからである.そこで,2番目の初期条
件(変位の速度)を使うことになる.計算したい量は
![]() なので,とりあえず
テーラー展開してみる.これを,
なので,とりあえず
テーラー展開してみる.これを,![]() の周りでテーラー展開すると,
の周りでテーラー展開すると,

![\begin{equation*}\begin{aligned}%
u(x,\Delta t) %
&\thickapprox u(x,0) +\psi(x...
...[ u(x+\Delta x,0)-2u(x,0)+u(x-\Delta x,0)\right] %
\end{aligned}\end{equation*}](img61.png)
![]() と
と![]() が得られたわけである.
が得られたわけである.![]() 以降は,
式(11)に従い,計算すればよい.
以降は,
式(11)に従い,計算すればよい.