3 数値計算の練習

3.1 微分方程式

オイラー法を使って，微分方程式を計算するプログラムを作成せよ．以下，詳細に説明し ているので，これを良く読めばプログラムの作成ができるはずである．

3.1.1 計算方法

次の微分方程式

$$\frac{\mathrm{d}y}{\mathrm{d}x}=\cos x$$ (1)

をオイラー法により計算する．ただし，初期条件は$x=0$の時$y=0$とする．当然，これは 数値計算するまでもなく，解は

$$y=\sin x$$ (2)

と分かっている．分かっているが，ここではコンピュータープログラムにより計算する． ここでの内容を良く理解すれば，通常解けない微分方程式でも，コンピューターにより計 算できることが分かるだろう．

コンピューターで微分方程式を計算する方法を示す．微分方程式の解を$y=f(x)$とする． すると，微分--正しくは導関数--は，

$$\frac{\mathrm{d}y}{\mathrm{d}x}\simeq\frac{\Delta y}{\Delta x}=\frac{f(x+\Delta x)-f(x)}{\Delta x}$$ (3)

と近似することができる．右辺の $\Delta x\rightarrow 0$の極限が微分 の値となる．したがって，元の微分方程式は

$$\frac{f(x+\Delta x)-f(x)}{\Delta x}\simeq\cos x$$ (4)

と書くことができる．これと，式(1)から，

$$f(x+\Delta x)\simeq f(x)+\Delta x\cos x$$ (5)

である．これがオイラー法で微分方程式を解くときの基本の式である．$\Delta x$の値を 小さくすると，この近似の精度が上がる．初期条件を上手に使うと，微分方程式の解の値 が芋づる式にわかる．仮りに， $\Delta x=0.001$とすると，次のような手順で計算する．

	(1)	$f(0.000)=0$	これは初期条件である．
	(2)	$f(0.001)=f(0.000)+0.001\times\cos(0.000)$	右辺は(1)の結果を利用する
	(3)	$f(0.002)=f(0.001)+0.001\times\cos(0.001)$	右辺は(2)の結果を利用する
	(4)	$f(0.003)=f(0.002)+0.001\times\cos(0.002)$	右辺は(3)の結果を利用する
	(5)	$f(0.004)=f(0.003)+0.001\times\cos(0.003)$	右辺は(4)の結果を利用する
		$\vdots$	これを繰り返す

(1)は初期条件なので計算するまでもない．そして，(1)の結果を利用すると，(2)の右辺 が計算でき，その左辺の値を決めることができる．同様に(2)の結果を利用すると，(3)の右辺 が計算でき，その左辺の値が決められる．これを繰り返すのである．すると，$x=0$の初 期条件からはじめて，任意の$x$まで$f(x)$の値を求めることができる．元の微分方程式 (1)の近似解が求まったことになる． $\Delta x=0.001$は 計算のステップ幅と呼ばれ，これを小さくするとさらに計算時間は必要になるが，計算精度が上がる．

例えば，これを4000回この計算を繰り返すと，微分方程式(1) の解が $y=f(0.000)$から$f(4.000)$まで計算できる．すなわち，0〜 $4\mathrm{[rad]}$ (229.1[度])までの値が $0.001\mathrm{rad}$(0.057[度])きざみで分かるのである．4000 回の計算なんか，コンピューターにとっては大したことはない．私のPCでは，計算と表示 に用した時間は，0.15秒である．コンピューターの計算速度には，本当に驚かされる．

3.1.2 計算アルゴリズム

計算の原理が分かったので，プログラミング方法を示す．計算のフローチャートは図 2のようになる．これにしたがって，プログラムを書けば良い．難 しいことは何もない．

まずは，計算のステップ幅$\Delta x$を決めなくてはならない．C言語では

	dx=4.0/4000;

と書く．プログラムではギリシャ文字は使えないので，ステップ幅をdxとしている． 解となる計算結果は後で利用することを考えて，配列に格納する方が良い．配列の先頭に は，初期条件を格納する．すなわち，

	x[0]=0.0;
	y[0]=0.0;;

とするのである．次にiの値を1〜4000まで変えて，

	x[i]=i*dx;
	y[i]=y[i-1]+dx*cos(x[i-1));

を繰り返し計算する．このように計算回数が決まっている繰り返しには，for文を使 うのが一般的である．

	for(i=1;i<=4000;i++){

	  ここに繰り返したい内容を書く．

	}

図 2: オイラー法のフローチャート．

3.2 連立方程式

次の連立方程式

$$a_{11}x_1+a_{12}x_2+a_{13}x_3 =b_1$$

$$a_{21}x_1+a_{22}x_2+a_{23}x_3 =b_2$$

$$a_{31}x_1+a_{32}x_2+a_{33}x_3 =b_3$$

を解くプログラムを作成する．解 $(x_1,\,x_2,\,x_3)$を求めろ--ということである．条 件は，以下の通りとする．

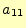• 9個の係数の$a_{11}$〜$a_{33}$はキーボードから入力する．
• 3個の非同次項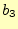$b_1$〜$b_3$もキーボードから入力する．
• 連立方程式の解 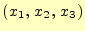$(x_1,\,x_2,\,x_3)$を表示する．

3.3 課題提出要領

提出方法は，次の通りとする．

期限	10月4日(木) 20:00
用紙	A4
提出場所	山本研究室の入口のポスト
表紙	表紙を1枚つけて，以下の項目を分かりやすく記述すること．
	授業科目名「計算機応用」
	課題名「課題　夏休みの宿題」
	5E    学籍番号    氏名
	提出日
内容	ソースプログラムは，プリントアウト，手書き，いずれもOKとする

なお，これは後期の成績に加味する．

ホームページ: Yamamoto's laboratory
著者: 山本昌志