2 非線型方程式
2.1 概要
非線形方程式2の近似解
この非線形方程式は,図1のように![]() のx軸と交わる点
に実数解を持つ.ここだけとは限らないが,少なくともこの交わる点は解である.この点
の値は,コンピューターを用いた反復(ループ)計算により探すことができる.ここの講義
では,次の2通りの方法で近似解を計算した.
のx軸と交わる点
に実数解を持つ.ここだけとは限らないが,少なくともこの交わる点は解である.この点
の値は,コンピューターを用いた反復(ループ)計算により探すことができる.ここの講義
では,次の2通りの方法で近似解を計算した.
- 2分法
- ニュートン-ラフソン法(ニュートン法)
2.2 二分法(bisection method)
2.2.1 計算方法
閉区間ならば,
実際の数値計算は,
![]() であるような2点
であるような2点
![]() から出発する.
そして,区間
から出発する.
そして,区間![]() を2分する点
を2分する点![]() に対して,
に対して,![]() を計算を行う.
を計算を行う.
![]() ならば
ならば![]() を
を![]() と置き換え,
と置き換え,
![]() ならば
ならば![]() を
を![]() と置き
換える.絶えず,区間
と置き
換える.絶えず,区間![]() の間に解があるようにするのである.この操作
を繰り返して,区間の幅
の間に解があるようにするのである.この操作
を繰り返して,区間の幅![]() が与えられた値
が与えられた値
![]() よりも小さく
なったならば,計算を終了する.解へ収束は収束率
よりも小さく
なったならば,計算を終了する.解へ収束は収束率![]() の一次収束である.
の一次収束である.
実際にこの方法で
を計算した結果を図2に示す.この図より,
- 長所
- 閉区間
![$ [a,b]$](img40.png) に解があれば,必ず解に収束する.間違いなく解
を探すので,ロバスト(robust:強靭な)な解法と言われている.
次に示すニュートン法とは異なり,連続であればどんな形の関数
でも解に収束するので信頼性が高い方法と言える.さらに,解の
精度も分かり便利である.解の誤差は,区間の幅
に解があれば,必ず解に収束する.間違いなく解
を探すので,ロバスト(robust:強靭な)な解法と言われている.
次に示すニュートン法とは異なり,連続であればどんな形の関数
でも解に収束するので信頼性が高い方法と言える.さらに,解の
精度も分かり便利である.解の誤差は,区間の幅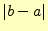 以下で
ある.
以下で
ある.
- 短所
- 収束が遅い(図6).一次収束である.
2.2.2 アルゴリズム
関数はあらかじめ,プログラム中に書くものとする.更に,計算を打ち切る条 件もプログラム中に書くものとする.そうすると,図 3のような2分法のフローチャートが考えられる.2.2.3 プログラム
このプログラムをしっかり理解せよ.テストで出題された場合,全く同じプログラムを書 く必要はない.同じアルゴリズムでも同一のプログラムになるとは限らない. 1 #include <stdio.h>
2 #define EPS (1.0e-15) /* precision of calculation */
3
4 double func(double x);
5
6 /*=============================================================*/
7 /* main function */
8 /*=============================================================*/
9 int main(void){
10 double a, b, c, test;
11 char temp;
12 int i=0;
13
14 do{
15 printf("\ninitial value a = ");
16 scanf("%lf%c", &a, &temp);
17
18 printf("initial value b = ");
19 scanf("%lf%c", &b, &temp);
20
21 test=func(a)*func(b);
22
23 if(test >= 0){
24 printf(" bad initial value !! f(a)*f(b)>0\n\n");
25 }
26 }while(test >= 0);
27
28 if(b-a < 0){
29 c=a;
30 a=b;
31 b=c;
32 }
33
34 while(b-a > EPS){
35
36 c=(a+b)/2;
37 if(func(c)*func(a) < 0){
38 b=c;
39 }else{
40 a=c;
41 }
42
43 i++;
44 }
45
46 printf("\nsolution x = %20.15f\n\n",c);
47
48 return 0;
49 }
50
51 /*=============================================================*/
52 /* definition function */
53 /*=============================================================*/
54 double func(double x){
55 double y;
56
57 y=x*x*x-3*x*x+9*x-8;
58
59 return y;
60 }
2.3 実数解のニュートン法(Newton's method)
2.3.1 計算方法
関数
まずは,この数列の漸化式を求める.関数![]() 上の点
上の点
![]() の接
線を引き,それとx軸と交点
の接
線を引き,それとx軸と交点![]() である.まずは,
である.まずは,![]() を求める
ことにする.点
を求める
ことにする.点
![]() を通り,傾きが
を通り,傾きが
![]() の直線の方
程式は,
の直線の方
程式は,
| (4) |
である.
となる.
計算の終了は,
 |
(6) |
の条件を満たした場合とするのが一般的である.
ニュートン法を使う上で必要な式は,式(5)のみで
ある.計算に必要な式は分かったが,数列![]() がどのように真の解
がどのように真の解![]() に収束
するか考える.
に収束
するか考える.![]() と真値
と真値![]() の差の絶対値,ようするに誤差を
計算する.
の差の絶対値,ようするに誤差を
計算する.
![]() を忘れないで,テイラー展開を用いて,計算を進める
と
を忘れないで,テイラー展開を用いて,計算を進める
と
 |
となる.
ニュートン法の特徴をまとめると次のようになる.
2.3.2 アルゴリズム
2分法同様,関数と計算を打ち切る条件はプログラム中に書くものとする.そ うすると,図5のようなニュートン法のフローチャー トが考えられる.2.3.3 プログラム
このプログラムをしっかり理解せよ.テストで出題された場合,全く同じプログラムを書 く必要はない.同じアルゴリズムでも同一のプログラムになるとは限らない.
ニュートン法では,導関数の計算が必要である.通常の方程式であれば,導関数は計算で
きるはずである.計算した導関数をプログラム中に記述する.
1 #include <stdio.h>
2 #include <math.h>
3 #define IMAX 50
4 #define EPS (1.0e-15) /* precision of calculation */
5
6 double func(double x);
7 double dfunc(double x);
8
9 /*================================================================*/
10 /* main function */
11 /*================================================================*/
12 int main(void)
13 {
14 double x[IMAX+10];
15 char temp;
16 int i=-1;
17
18 printf("\ninitial value x0 = ");
19 scanf("%lf%c", &x[0], &temp);
20
21 do{
22 i++;
23 x[i+1]=x[i]-func(x[i])/dfunc(x[i]);
24 }while(i<=IMAX && fabs((x[i+1]-x[i])/x[i]) >= EPS);
25
26 if(i>=IMAX){
27 printf("\n not converged !!! \n\n");
28 }else{
29 printf("\niteration = %d\nsolution x = %20.15f\n\n",i,x[i+1]);
30 }
31
32 return 0;
33 }
34 /*================================================================*/
35 /* definition function */
36 /*================================================================*/
37 double func(double x)
38 {
39 double y;
40
41 y=x*x*x-3*x*x+9*x-8;
42
43 return y;
44 }
45 /*================================================================*/
46 /* definition derived function */
47 /*================================================================*/
48 double dfunc(double x)
49 {
50 double dydx;
51
52 dydx=3*x*x-6*x+9;
53
54 return dydx;
55 }
2.4 ニュートン法と2分法の比較
2.4.1 解への収束速度
図6に,二分法とニュートン法の解への近 づき具合を示す.二分法に比べ,ニュートン法が解への収束が早いことがわかる.前者は 二次収束で,後者は一次収束であることがグラフより分かる.二分法は,10回の計算で,二分法に比べて,ニュートン法は収束が早く良さそうであるが,次に示すように解へ収束 しない場合があり問題を含んでいる.
2.5 ニュートン法の問題点
アルゴリズムから,2分法は解に必ず収束する.ただし,この方法は,収束のスピードが 遅く,それが欠点となっている.一方,ニュートン法は解に収束するとは限らない.初期 条件に依存する場合がある.厳密にその条件を求めるのは大変なので,初期条件により収 束しない実例を示す.非線形方程式
| (8) |
の解を計算することを考える.これは,初期値のより,収束しない場合がある.例えば初 期値
このようにニュートン法は解に収束しないで,振動する場合がある.こうなる と,プログラムは無限ループに入り,永遠に計算し続ける.通常は反復回数の上限を決め ,無限ループを防ぐ.ニュートン法を使う場合は,この反復回数の上限は必須である.
実際には収束しない場合のほうが稀であるので,ニュートン法は非常に強力な 非線型方程式の解法である.ただ,反復回数の上限を決めることを忘れてはならない.
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成19年7月25日
![\includegraphics[keepaspectratio, scale=0.7]{figure/function_solution/ShapeOfFunction.eps}](img14.png)
![\includegraphics[keepaspectratio, scale=0.7]{figure/function_solution/NibunMethod.eps}](img52.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/flow_chart/flow_nibun.eps}](img53.png)
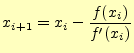
![\includegraphics[keepaspectratio, scale=0.7]{figure/function_solution/NewtonMethod.eps}](img95.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/flow_chart/flow_newton.eps}](img96.png)
![\includegraphics[keepaspectratio, scale=0.7]{figure/Graph/Bisection_Newton.eps}](img98.png)
![\includegraphics[keepaspectratio, scale=0.4]{figure/comv_hasan/hasan.eps}](img102.png)
![\includegraphics[keepaspectratio, scale=0.4]{figure/comv_hasan/comb.eps}](img103.png)