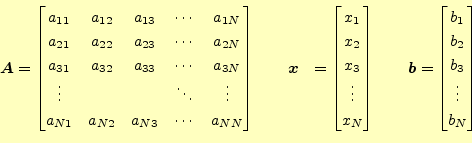
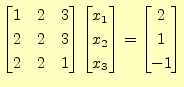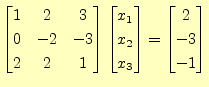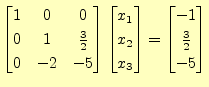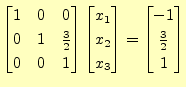連立1次方程式(Linear Equations)は,次のような形をしている.
式(25)は行列とベクトルで書くと,式がすっきりして
考えやすくなる.書き直すと,
である.それぞれの行列とベクトルは,
を表す.
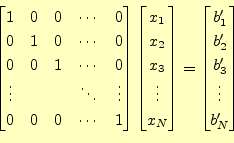
通常,連立1次方程式(25)は
と書き表せる.このようにすると,見通しがかなり良くなる.
ガウス・ジョルダン(Gauss-Jordan)法というのは,連立方程式
(28)を次にように変形させて,解く方法である.
この式から明らかに,求める解
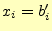 となる.これをどうやって求めるか?.
コンピューターで実際に計算する前に,人力でガウス・ジョルダン法で計算してみる.例
として,
となる.これをどうやって求めるか?.
コンピューターで実際に計算する前に,人力でガウス・ジョルダン法で計算してみる.例
として,
をガウス・ジョルダン法で解を求める.
解くべき,方程式
 1行
1行
2行 1行
1行
3行 1行
1行
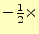 2行
2行
1行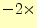 2行
2行
3行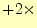 2行
2行
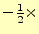 3行
3行
 3行
3行
これで,ガウス・ジョルダン法による対角化の作業は完了である.これか
ら,
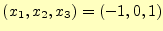 と分かる.
ピボット選択は行わないで,逆行列も求めないのガウス・ジョルダン法で連立方程式を計
算するプログラムを示す.このプログラムの動作は,次の通りである.
と分かる.
ピボット選択は行わないで,逆行列も求めないのガウス・ジョルダン法で連立方程式を計
算するプログラムを示す.このプログラムの動作は,次の通りである.
- 仮引数「n」は,解くべき連立方程式の未知数の数である.
- 仮引数の配列「a」と「b」は,係数行列
 と非同次項
と非同次項
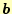 である.
値は,呼び出し元からにアドレス渡しで送られる.
である.
値は,呼び出し元からにアドレス渡しで送られる.
- 係数行列は,配列「a[1][1]」〜「a[n][n]」に格納されている.
- 非同次項は,配列「b[1]」〜「b[n]」に格納されている.
- 連立方程式の解
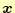 は,配列「b[1]」〜「b[n]」に格納される.
は,配列「b[1]」〜「b[n]」に格納される.
- このプログラムでの処理が終了すると,配列「a[1][1]」〜「a[n][n]」は単位
行列になる..
/* ========== ガウスジョルダン法の関数 =================*/
void gauss_jordan(int n, double a[][100], double b[]){
int ipv, i, j;
double inv_pivot, temp;
for(ipv=1 ; ipv <= n ; ipv++){
/* ---- 対角成分=1(ピボット行の処理) ---- */
inv_pivot = 1.0/a[ipv][ipv];
for(j=1 ; j <= n ; j++){
a[ipv][j] *= inv_pivot;
}
b[ipv] *= inv_pivot;
/* ---- ピボット列=0(ピボット行以外の処理) ---- */
for(i=1 ; i<=n ; i++){
if(i != ipv){
temp = a[i][ipv];
for(j=1 ; j<=n ; j++){
a[i][j] -= temp*a[ipv][j];
}
b[i] -= temp*b[ipv];
}
}
}
}
ホームページ: Yamamoto's laboratory
著者: 山本昌志
Yamamoto Masashi
平成19年11月27日