1 物理学における対称性
ここでは,物理法則を記述するときに,ベクトルを使う理由を述べる.数学と異なり,物 理学ではベクトルを使わなくてはならない特別な理由がある.それは,座標軸の平行移動 や回転に対して,物理の基本法則を示す方程式が変わらないということに関係する.電磁 気学でも,このことは成り立つが,力学でそれを示す.これから学習する電磁気学方程式 は複雑なので,最初の例としてふさわしくない.そこで,方程式がが単純な力学を使うこ とにする.このあたりの話の種本は,「ファインマン物理学 I 力学」 []である.
1.1 対称性
力学や電磁気学,さらに他の物理学の分野の基本法則は,平行移動や回転に対して対称で ある.ここで,対称と言う意味は,ファインマンはヘルマン・ワイルの言葉を借りてひとつのものにある操作をしたとき,もとと同一に見えるならば,そのものは対称である という.例えば左右対称な花瓶があるとき,それを鉛直軸のまわりに180°まわすと,ま えと同じように見える.と言っている [1].電磁気学を含んだ物理の基本法則が,平 行移動や回転に対して対称であることは,直感的に理解できる.それは,我々が住んでい る世界には座標をきめる特別な原点はないということと,座標軸を決める特別な軸がない ことからも分かる.このことを,「空間は等方である」という.本当に,そうなのか? 特別な原点や特別な軸を示す現象を捜してみよう.見付からないはずである.
1.2 平行移動
それでは平行移動に関して,物理の基本法則である力学が対称であることを示そう.ベク トルを使わない力学の方程式はである.問題は,この座標の原点と軸の方向である.まずは,座標の原点としてどこを選 んでも方程式が同じであることを示す.
これから,原点はどこでも良いことを示そう.A君とA![]() 君がある質点の運動を異
なる原点を使って観測したとする.A君の座標を
君がある質点の運動を異
なる原点を使って観測したとする.A君の座標を![]() ,A
,A![]() 君の座標を
君の座標を
![]() とする(図1).それぞれは,
とする(図1).それぞれは,
| (2) |
の関係がある.これは,原点は異なるが,軸の方向は一致していると言っている.A君の 座標系で,運動方程式(1)が成り立っているとする.同じよう に,A
は成り立つのであろうか?
質点にかかる力は,A君から見てもA![]() 君ら見ても同じである.そして,力の各方向の成分は,全ての力に力の軸と座標の軸との方向余弦(
君ら見ても同じである.そして,力の各方向の成分は,全ての力に力の軸と座標の軸との方向余弦(
![]() )をかけたものである.これと両者の座標軸の方向が一致しているとことから,
)をかけたものである.これと両者の座標軸の方向が一致しているとことから,
となる.両者の力の各方向の成分は同一になる.これは,直感的に当たり前である.
次に,式(1)の加速度を考える.A![]() 君の座標系での加速度は,
君の座標系での加速度は,
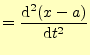 |
||
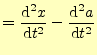 |
||
| 原点の距離 |
||
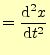 |
(5) |
となる.
となる.原点が異なっても,加速度は同一となる.
式(4)と(6)より,A君の座標で運動方程式
(1)が成り立てば,A![]() 君でも同じような運動方程式
(3)が成り立つ.これは,運動方程式は,座標の原点と
は関係なく成り立つことを言っている.座標の原点はどこをとってもよいのである.
君でも同じような運動方程式
(3)が成り立つ.これは,運動方程式は,座標の原点と
は関係なく成り立つことを言っている.座標の原点はどこをとってもよいのである.
1.3 回転
ニュートンの運動方程式--物理の基本法則--が軸の回転に対しても対称でことを確認す る.図2のように,原点は同じで,z軸を回転軸としてである.座標を回転させたときのA
が成り立つか?--を調べる.もしこれが成り立てば,A君の座標系でも,A
対称性を調べるために,座標の変換と力の変換の仕方を考えなくてはならない.まずは, 座標の変換であるが,これは簡単である.図2から明らかに,これら 2つの座標系は
の関係がある.もう少し,分かり易く書くと
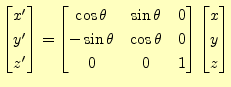 |
(10) |
となる.これから,ただちに式(7)と式 (8)のそれぞれの左辺には,
と言う関係があることがわかる.行列に書き直しているが,同じである.
残りは,座標が回転した場合,力の変化の様子を調べることにする.ただちに分かることは,A君とA![]() 君が見る力の
君が見る力の![]() 方向成分は,
方向成分は,
とまったく同一になる.
| (13) |
ここで,
となる.一方,A
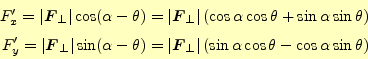 |
(15) |
となる.式(14)と見比べると,これは
と書き直すことができる.式(12)と式(16)より, A君とA
となることがわかる.
式(7)と式 (8)のそれぞれの左辺の加速度の変換の式は式 (11)に示している.それぞれの右辺,すなわち力の関係は,式 (17)のとおりである.これらの式(11)や式 (17)は,座標変換にともなう加速度や力の変換仕方を表している のである.これらの式から,座標の回転によって,加速度の成分--座標の成分--と力の 成分が,同一の行列によって変換されることがわかる.同じ変換を受けるということであ る.ということは,式(7)が成立すれば,式 (8)が成り立つと言っている.これらの式--ニュート ンの運動方程式--の形は同一である.したがって,ニュートンの運動方程式は座標の回 転に対して,対称である.これは,座標軸を勝手にとっても,ニュートンの運動方程式は 成立すると言っている.これは,重要な事実である.
ここでは,
![]() 軸を中心に回転させたが,
軸を中心に回転させたが,
![]() 軸でも
軸でも
![]() 軸でも同じように対称と
なる.
軸でも同じように対称と
なる.
![]() 軸を中心に回転させて,
軸を中心に回転させて,
![]() 軸を中心に回転させるように回転を2回施し
ても,同じように対称なるはずである.回転を2回施すことは,任意の方向を軸として,
回転を1回施す作用と同じである.したがって,任意の方向を軸にして,回転させても,
ニュートンの運動方程式は対称となる.ニュートンの運動方程式は,回転に対して,対称
となっている.
軸を中心に回転させるように回転を2回施し
ても,同じように対称なるはずである.回転を2回施すことは,任意の方向を軸として,
回転を1回施す作用と同じである.したがって,任意の方向を軸にして,回転させても,
ニュートンの運動方程式は対称となる.ニュートンの運動方程式は,回転に対して,対称
となっている.
1.4 ベクトル
物理学の基本法則は,座標の平行移動や回転に対して,その方程式の形は変わらない.す べての基本法則はそのように書かれているはずである.何度も言うようだが,これは,我々 が住んでいる世界には特別な原点や軸がないことを表している.単純な例として,ニュー トンの運動方程式が,そのようになっていることを先に示した.これから学習する電磁気 学も,座標の平行移動や回転に対して,方程式の形は変わらない.これまで,示してきた加速度や力は,ベクトルの例である.これは,ある空間に固定され た一本の矢のように考えることができる.それは方向と大きさを持っている.それは,座 標系に関係なく存在している.この幾何学的な形をもつ1本の矢がどのように変化するの か?--を考えるのが物理学である.だからこそ,平行移動や回転に対して,方程式の形が 変わらなかったのである.
実際に問題を解く場合,適当に座標の原点と軸を決めて,基本方程式を解くことにな
る.この場合,![]() のように3つの数値が必要となる.この3つの数値の組をひとつ
の記号
のように3つの数値が必要となる.この3つの数値の組をひとつ
の記号
![]() で表すことにする.これをベクトルと言う.また,回転と平行移動を施し
た別の座標系を使うと
で表すことにする.これをベクトルと言う.また,回転と平行移動を施し
た別の座標系を使うと
![]() のように異なる組の数値が必要となる.この場合も同じ,
記号
のように異なる組の数値が必要となる.この場合も同じ,
記号
![]() を使う.座標系により,成分は異なるが同じ記号を使うことになる.
許されるのは,
を使う.座標系により,成分は異なるが同じ記号を使うことになる.
許されるのは,
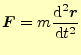 |
(18) |
がどちらの座標系を使っても,同じ式になるからである.
ベクトルの成分がどのような性質があるかは,最後に述べる.
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成19年4月10日
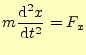
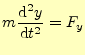
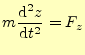
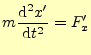
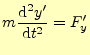
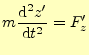
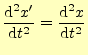
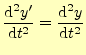
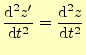
![\includegraphics[keepaspectratio, scale=1.0]{figure/move_para.eps}](img37.png)
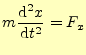
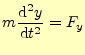
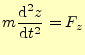
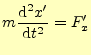
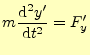
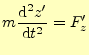
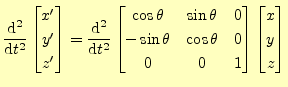
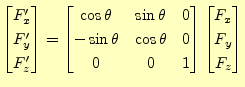
![\includegraphics[keepaspectratio, scale=1.0]{figure/rot_xy_vec.eps}](img81.png)