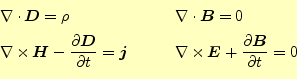3 電磁気学の基本法則
古典物理学の2つの柱は,ニュートン力学と電磁気学である.いずれもベクトルをつかっ た微分方程式が書かれることが多く,ニュートン力学では| (1) | ||
| ここで,
|
||
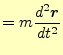 |
(2) |
となる.これが Newtonの運動の第2法則(Newton's Second Law of Motion)である.通常 はこれを積分して,運動を求めることになる2.
これに対して,電磁気学の法則は,
と書かれる4組の連立の微分方程式である.これをマクスウェルの方程式(Maxwell equations)という.ここで,
| 記号 | 物理量 | 単位 | スカラー/ベクトル |
|
|
電束密度 | [
|
ベクトル |
|
|
磁束密度 | [T]あるは[
|
ベクトル |
|
|
磁場(の強さ) | [
|
ベクトル |
|
|
電場(の強さ) | [
|
ベクトル |
| 電荷密度 | [
|
スカラー | |
|
|
電流密度 | [
|
ベクトル |
である.こんなものはまだ理解する必要はない.この授業の最後で理解すべきものとなる. ただ,基本方程式というものがあることは分かって欲しい.
力学では,基本方程式が与えられてから,それを問題に適用することを学習する.それに 対して,ここでの電磁気学では,最後の方に基本方程式を導くことになる.力学の基本方 程式は,直感的にある程度理解できるので,最初に基本法則を教えるとが可能である.一 方,不幸なことに,電磁気学の基本式(3) は複雑で,直感的に理解 することは不可能である.そのため,基本式にたどり着く前に,いろいろと修行する方法 がとられる.
話は変わるが,電気回路のもっとも基本的な法則であるオームの法則やキルヒホッフの法 則もこのマクスウェルの方程式から,ある近似をして導くことができる.電気回路といえ ども電磁気的な現象なので,マクスウェルの方程式から計算できるのである.ただ,計算 が大変なので,近似であるオームの法則を使う.通常であれば,それで十分な精度を得る ことができる.流体力学でも,似たような話がある.分子の衝突の計算をしないで,流体 の方程式を計算するのと同じ状況にある.
おもしろいことに,回路の動作が高速になるとオームの法則ではだめな場合が生じている. 高速のCPUの設計にオームの法則ではなく,マクスウェルの方程式が使われることがある.
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成19年7月12日