平成17年度横浜国立大学工学部編入試験に出題された問題である。
3本の棒(src, dst, work)が立っており、そのうち、左端の棒(src)に大きさの異なるn枚
の円盤が、大きさの順に差し込まれている。円盤を一枚ずつ、棒から棒へ移動させ、最終
的にsrcにあるn枚の円盤すべてを中心の棒(dst)に移動させるアルゴリズムを考える。た
だし、各円盤は、各棒において、常により小さい円盤がより大きな円盤の上に乗るように
しか移動できず、すべての円盤が移動した結果もまた、大きさの順に積まれていなければ
ならないとする。この制約を満たす移動手順を求めるアルゴリズムは「ハノイの塔」と呼
ばれている。
下記のプログラムは、「ハノイの塔」アルゴリズムをC言語で実現した例である。ここで、
例えば"src->work"という出力は、srcにある一番上の円盤を、workの一
番上に移動させることを意味する。また、任意のnを#define DISK_NUM nとし
て指定している。
1 #include <stdio.h>
2 #define DISK_NUM 3
3
4 void hanoi(int n, char* a, char* b, char* c){
5
6 if(0==n)return;
7
8 hanoi(n-1, a, c, b);
9 printf("%4s -> %4s \n", a, b);
10 hanoi(n-1, c, b, a);
11 }
12
13 int main(){
14 int n = DISK_NUM;
15 hanoi(n, "src", "dst", "work");
16 return 0;
17 }
- [問1]
- 関数hanoi()中では、hanoi()が2回呼ばれている。このように、
関数の中で自分自身を関数として呼び出すことを「_(a)_呼び出し」とい
う。(a)に当てはまる言葉を答えなさい。
- [問2]
- このプログラムを実行すると下記の出力が得られた。(b), (c)の行に相当
する結果を答えなさい。ただし、空白(スペース)は明記する必要はない。
- [問3]
- #define disk_num 4 とした場合に、出力される行数は_(d)_行であ
る。(d)に相当する数を答えなさい。
- [問4]
- 任意のnについて、初期状態からdstへ円盤がすべて移動するまでに要する
hanoi()の呼び出し総数(e)と、ディスクの移動回数(f)を、それぞれn
を用いてできるだけ簡潔な式で表しなさい。
再帰呼び出しを使って、ハノイの塔のパズルを解くためには、以下の手順を踏めばよい。
- srcにあるn枚の円盤のうち、上のn-1枚をworkに移す。
- srcに残っている一番下の円盤をdestに移動させる。
- 以上で、一番下の処理が終わり、処理の終わっていないn-1枚の円盤はwarkにある。
これは、円盤の数が1枚減った最初の状態と同じである。したがって、最初から同
じことを繰り返す。
問題で与えられたプログラムは、この手順を踏むようになっている。プログラムの内容が
理解できれば、以下の解答は分かるはずである。
- [問1]
- 再帰
- [問2]
- dst -> work
work -> dst
- [問3]
- 15
- [問4]
- 円盤が
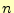 枚の時の関数hanoi()の呼び出し総数
枚の時の関数hanoi()の呼び出し総数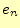 は、
は、
となる。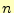 枚の時、1回呼び出した後、
枚の時、1回呼び出した後、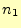 枚で2度呼び出しているから
である。この数列の一般項を求めることになるが、そのために、
枚で2度呼び出しているから
である。この数列の一般項を求めることになるが、そのために、
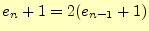 |
(15) |
と変形する。これは等比級数なので、簡単に計算できる。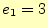 なので、
なので、
となる。したがって、関数hanoi()の呼び出し総数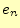 は、
は、
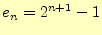 |
(17) |
となる。
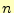 枚の時の円盤の移動回数
枚の時の円盤の移動回数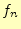 は、
は、
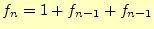 |
(18) |
となる。関数hanoi()を1回呼び出すと、必ず円盤の移動が一回発生す
る。加えて、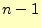 枚の呼び出しを2回行っているからである。この式を変形すると、
枚の呼び出しを2回行っているからである。この式を変形すると、
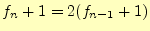 |
(19) |
となる。これは等比数列なので、一般項は簡単に求められる。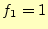 なの
で、
なの
で、
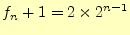 |
(20) |
となる。したがって、円盤の移動回数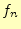 は、
は、
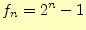 |
(21) |
と表すことができる。
ホームページ: Yamamoto's laboratory
著者: 山本昌志
Yamamoto Masashi
平成19年8月22日
![\fbox{\parbox[t]{40mm}{
\texttt{ src -> dst}\\
\texttt{ src -> work}\\
\rul...
...rc}\\
\rule{8mm}{0.5pt}(c)\rule{8mm}{0.5pt}\\
\texttt{ src -> dst}\\ \\
}}](img89.png)
![]() 枚の時の円盤の移動回数
枚の時の円盤の移動回数![]() は、
は、