誘電体があっても静電場では,
を満足する.もちろん,
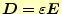 が成り立つ.とくに,図1のように一部の
領域の誘電率が 不連続に変化--誘電体が連続的に変化しない--場合,
が成り立つ.とくに,図1のように一部の
領域の誘電率が 不連続に変化--誘電体が連続的に変化しない--場合,
となる.この場合でも,
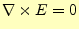 が成り立つので,電場はスカラーポテンシャル
が成り立つので,電場はスカラーポテンシャル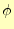 の勾配と書け
る.
の勾配と書け
る.
もっと言えば,誘電体が連続に変化しても,静電場の問題ではポテンシャルの計算に帰着
できる.なぜならば,静電場の問題はいつでも
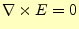 が成り立つからである.
が成り立つからである.
式(2)と式(3)を満足させるためには,
となる必要がある.もし,それぞれの領域に真電荷が無いとすると,ポテンシャルの方程
式は,
となる.ただし,この方程式を解く場合それぞれの領域で計算する必要がある.そして,
誘電率が異なる二つの境界でポテンシャルの値を同一にしなくてはならない.これは,そ
れぞれの領域でラプラス方程式を解く問題で,境界条件の設定が重要になる.たぶん,誘
電体の境界でポテンシャルを設定することは困難であろう.
そこで,別々にラプラス方程式を解くのではなく,式(1)とス
カラーポテンシャルの式(4)から,直接得られる
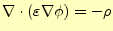 |
(8) |
を計算する方がよい.
図 1:
ここで取り扱う問題;誘電体が不連続に変化する領域の数値計算.
|
|
ホームページ: Yamamoto's laboratory
著者: 山本昌志
Yamamoto Masashi
平成19年8月20日