次のような条件の静電場を計算する方法について検討を行う.
- 計算領域に真電荷は無い.
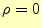 |
(9) |
- 誘電率は不連続に変化する.
このような条件のもと,差分法と有限要素法(変分法),有限積分法の数値計算について簡
単にコメントする.
ここで計算する静電場の方程式は,式(1)とスカラーポテンシャルか
ら,
導くことができる.これは2階の微分方程式になっており,差分の式はとなりの
要素を含めた計算になる.隣の要素まで含めるとなると,一つの式の中に誘電率が異なる
部分が生じる(図2).この取り扱いは面倒である.
あるいは,それぞれの誘電体中でラプラス方程式
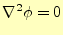 |
(11) |
を計算してもスカラーポテンシャルを得ることもできる.しかし,実際この式を計算する
こは,簡単ではない.二つの誘電体の境界条件が設定できないからである.
以上のことから,差分法はこのように誘電率が異なる静電場の計算には適さない.
図 2:
差分法のメッシュとノード.誘電率の異なる部分を横切るので,取り扱いが
困難二になる.
|
|
一つの要素で完結すると言うことから,変分法を基礎とする有限要素法の方が,このよう
な問題に適する.変分法とラプラス方程式の関係は,付録Aを見よ.
次の汎関数2
の第一変分がゼロの時の,ラプラス方程式になる(付録A参照).この第一変分がゼロになる
 が求める--ことが静電場の問題となる.ここで重要なことは,被積分関数が1階の
微分になっていることである.後で述べることになるが,1階の微分だと一つの要素の隣
接する4つのポテンシャルから計算できる.
が求める--ことが静電場の問題となる.ここで重要なことは,被積分関数が1階の
微分になっていることである.後で述べることになるが,1階の微分だと一つの要素の隣
接する4つのポテンシャルから計算できる.
汎関数は3次元の積分であるが,これ以降,二次元で話を進める.三次元だと図を書くの
が大変だし,式も長くなる.また,二次元であろうが三次元であろうが本質的に同じで,
三次元への拡張も簡単である.
任意の領域で式(12)の積分は,図3正方形メッシュに分割して近似計算できる.
四角形要素ごとに積分を行い,すべてを足しあわせることで全体の汎関数![$ U[\phi]$](img33.png) の値を計算
するのである.積分は要素ごとに行うので,誘電率が変化しても要素内で同一になるよう
にしておけば計算は容易になる.
の値を計算
するのである.積分は要素ごとに行うので,誘電率が変化しても要素内で同一になるよう
にしておけば計算は容易になる.
図 3:
有限要素法のメッシュとノード.おのおの要素ごとに積分を行う.
|
|
式(13)の計算は,四角形要素内での積分を行わなくてはならない.ひとつの
四角形要素を図4のようにし,それを4分割して積分を行う.まず1
番目の部分の勾配は
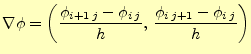 |
(14) |
となる.したがって,1番目の積分は,
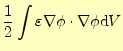 |
![$\displaystyle =\frac{\varepsilon_{i+1/2\,j+1/2}}{8}\left[ (\phi_{i+1\,j}-\phi_{i\,j})^2+ (\phi_{i\,j+1}-\phi_{i\,j})^2 \right]$](img37.png) |
(15) |
となる.同じことを2番目,3番目,4番目の領域に対して行い,合計すると 番目の
エレメントの積分値が計算できる.
番目の
エレメントの積分値が計算できる.
領域全体 の積分は,
の積分は,
となる.
図:
有限要素法のひとつの 番目のエレメントとポテンシャル.要素内で誘
電率は一定で,
番目のエレメントとポテンシャル.要素内で誘
電率は一定で,
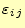 である.積分は1〜4の領域に分け
て行う.
である.積分は1〜4の領域に分け
て行う.
|
|
付録Aで述べたように,式(17)の個々の
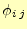 を変化させても,汎関数
を変化させても,汎関数![$ U[\phi]$](img51.png) の値が変化しないとき,正しい
ポテンシャル
の値が変化しないとき,正しい
ポテンシャル
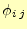 となる.ようするに,境界条件を満たしつつ,静電場のエネルギー
となる.ようするに,境界条件を満たしつつ,静電場のエネルギー
![$ U[\phi]$](img53.png) が停留値--ここでは極小値--をとるポテンシャル
が停留値--ここでは極小値--をとるポテンシャル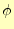 を探せということである.
を探せということである.
式(17)汎関数が停留値になる条件は,
となる.これらの式のうち,もっとも一般的な
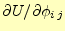 を計
算する.
を計
算する.
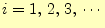 ,
,
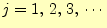 と
と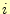 と
と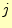 を変化させれば,
すべての式を得ることができる.ただし,境界に接する要素は気をつけなくてはならない.
を変化させれば,
すべての式を得ることができる.ただし,境界に接する要素は気をつけなくてはならない.
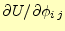 を計算するために,式(17)の
を計算するために,式(17)の
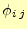 の周りの4つの要素に関わる項を書き出すと
の周りの4つの要素に関わる項を書き出すと
となる.これは,式(17)の和の計算の部分を展開しただけであるが,
図5を見ればこうなることが分かるだろう.この結果を用いると,
が得られる.これは,計算領域内部のすべてのポテンシャルについて成り立つ.したがって,
式(20)は,
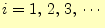 ,
,
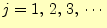 とする
ことにより連立方程式となっていることが理解できるだろう.境界条件としてポテンシャルの
値が与えれれているところをのぞいて,この連立方程式を解けばよい.
とする
ことにより連立方程式となっていることが理解できるだろう.境界条件としてポテンシャルの
値が与えれれているところをのぞいて,この連立方程式を解けばよい.
図:
汎関数の積分計算のうち,ポテンシャル
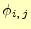 が関係する要素.
が関係する要素.
|
|
領域の境界でポテンシャルが与えられていない場合,その場所では電場が境界と垂直にな
る3.これは,式(25)から保証される.
連立方程式(20)を見ると,ほとんど差分の式と同じである.もし,誘
電率が一定とすると差分の式と全く同一になる.
もちろん,有限積分法も適用できる.時間がないので,その解説は行わない.
ホームページ: Yamamoto's laboratory
著者: 山本昌志
Yamamoto Masashi
平成19年8月20日
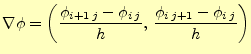
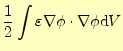
![\begin{multline}
\int_{\Omega_{ij}}\varepsilon\nabla \phi \cdot\nabla \phi \mat...
...i\,j+1}-\phi_{i\,j})^2+
(\phi_{i+1\,j+1}-\phi_{i+1\,j})^2\right]
\end{multline}](img39.png)
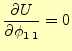
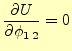
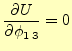
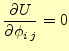
![]() を計算するために,式(17)の
を計算するために,式(17)の
![]() の周りの4つの要素に関わる項を書き出すと
の周りの4つの要素に関わる項を書き出すと