[Previous: 2 数値計算方法] [Up: 誘電率が異なる場合の静電場の数値計算] [Next: 参考文献]
汎関数が停留値になる条件は,その第一変分がゼロである.式(21)の
凡関数の第一変分![]() は
は
![$\displaystyle \delta U=\left\{\lim_{\alpha\rightarrow 0}\frac{U[\phi+\alpha v]-U[\phi]}{\alpha}\right\}\alpha$](img88.png) |
(20) |
| (22) |
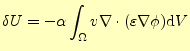 |
(24) |
ここでの結論は,「式(21)の汎関数の第一変分をゼロにすることと,
式(27)の微分方程式と解くことは等価」である.ようするに,式
(27)の微分方程式の解は,式(21)の積分が停
留値--しばしば極小値--になるような関数![]() と同一である.
と同一である.
式(21)の積分は,静電場のエネルギーになっている.境界条件を満た
しつつ,このエネルギーが最低になる状態が実際の状態である.ここでは,この積分が極
小になる![]() を計算することになる.
を計算することになる.
この静電場も最小エネルギーの問題になっている.しばしば,物理的に安定な状態はエネ ルギーが最低になる.この静電場の問題もその例の一つである.