一般化固有値問題は、以下の形で与えられる。
 |
(1) |
共役勾配法ではこのような固有値問題の最小固有値を求められる。
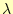 は,Raylaigh商から求められる.
は,Raylaigh商から求められる.
 |
(2) |
最急勾配方向1
 を以下に示す.
を以下に示す.
 |
(3) |
固有ベクトルは以下のように反復法で求められる.
| |
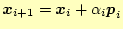 |
(4) |
| |
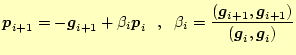 |
(5) |
ただし,
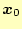 をランダム関数などを使って適当に決め,
をランダム関数などを使って適当に決め,
 として,
として,
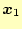 から計算し始める.
から計算し始める.
ここで,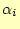 を求めなくてはいけないが,これは
を求めなくてはいけないが,これは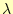 が最小になる
ように選べばいいので,
が最小になる
ように選べばいいので,
 |
(6) |
すなわち,
![$\displaystyle \frac{\partial }{\partial \alpha_i} \left( \frac{(\boldsymbol{x}_...
..._i, \boldsymbol{B}[\boldsymbol{x}_i + \alpha_i \boldsymbol{p}_i] )} \right) = 0$](img14.png) |
(7) |
となるように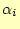 を決める.ここで,これを計算すると,
を決める.ここで,これを計算すると,
 |
(8) |
ただし,
と置いた.
ここで, は2つでてきたが,実際は
は2つでてきたが,実際は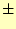 のところを
のところを にする.
つまり,
にする.
つまり,
 |
(9) |
である.
ここで,手順をまとめると次のようになる.
-
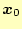 をランダム関数などを使い,適当に決める.
をランダム関数などを使い,適当に決める.
-
 とする.
とする.
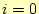
-

-

- 収束判定をして,収束が十分でなければ
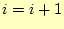 として,4に戻る.
として,4に戻る.
これで,最小の固有値と固有ベクトルが求められる.
ホームページ: Yamamoto's laboratory
著者: 夏井拓也
natui takuya
平成17年12月22日
![]() は,Raylaigh商から求められる.
は,Raylaigh商から求められる.


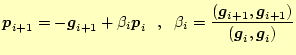
![]() を求めなくてはいけないが,これは
を求めなくてはいけないが,これは![]() が最小になる
ように選べばいいので,
が最小になる
ように選べばいいので,

![$\displaystyle \frac{\partial }{\partial \alpha_i} \left( \frac{(\boldsymbol{x}_...
..._i, \boldsymbol{B}[\boldsymbol{x}_i + \alpha_i \boldsymbol{p}_i] )} \right) = 0$](img14.png)

