2 ビットシフトの意味

2.1 基数Nの場合

10進数を10倍、100倍、1000倍、$\cdots$するのは簡単である。$10^{n}$倍するためには、 左にゼロを$n$個付ければ良い。これは、左シフトである。同様に$1/10$倍、$1/100$倍、 $1/1000$倍、$\cdots$するのは簡単である。$10^{-n}$倍するためには、小数点の位置を $n$個左に寄せれば良い。これは右シフトである。

16進数の場合も同じである。たとえば、$(EF35)$を $(16)_{10}=(10)_{16}$倍や $(16)^2_{10}=(10)^2_{16}$倍、 $(16)^{-1}_{10}=(10)^{-1}_{16}$倍や $(16)^{-2}_{10}=(10)^{-2}_{16}$倍すると

$$\begin{aligned}(EF35)_{16}\times(16^2)_{10}&=(EF35)_{16}\times(... ...0}&=(EF35)_{16}\times(0.01)_{16} &=(EF.35)_{16} \end{aligned}$$

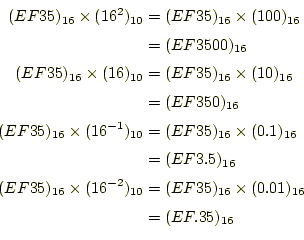となる。やはり、右や左にシフトさせれば良い。

2進数の場合も全く同じである。この場合、$2^{n}$の計算が簡単である。$n$が正の整数 の場合、左に$n$ビットシフトさせる。一方、$n$が負の整数の場合、$n$の絶対値分、右 にシフトさせる。

$$\begin{aligned}(110011)_{2}\times(2^2)_{10}&=(110011)_{2}\times... ...}&=(110011)_{2}\times(0.01)_{2} &=(1100.11)_{2} \end{aligned}$$

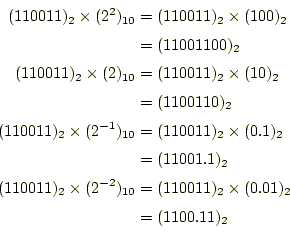2.2 CASL IIの場合

2.2.1 ビットシフト

CASL IIで取り扱う16ビットの整数を$2^n$倍する事を考える。もし、その16ビットが正 で有れば、それは簡単である。先に示したように、$n$ビット右や左にシフトさせれば良 い。

問題は、符号付き整数で、第15ビットが1の負の場合である。これは、実例を示した方が 分かりやすい。たとえば、 $(-12)_{10}$を2倍と4倍する事を考える。2倍すると $(-24)_{10}$で、4倍すると $(-48)_{10}$である。それぞれを、2の補数で取り扱うと、 となる。

$$(-12)_{10} \rightarrow(1111\; 1111\; 1111\; 0100)$$

$$(-24)_{10} \rightarrow(1111\; 1111\; 1110\; 1000)$$

$$(-48)_{10} \rightarrow(1111\; 1111\; 1101\; 0000)$$

従って、CASL IIの符号付き16ビット整数の場合、$2^n$する場合は、左に$n$ビットシフ トさせて、空いたビットに0を入れれば良い。

次に、1/2倍と1/4倍する事を考える。すると

$$(-12)_{10} \rightarrow(1111\; 1111\; 1111\; 0100)$$

$$(-6)_{10} \rightarrow(1111\; 1111\; 1111\; 1010)$$

$$(-3)_{10} \rightarrow(1111\; 1111\; 1111\; 1101)$$

となる。この場合も右に$n$ビットシフトさせれば良いのであるが、空いたビットには1を 入れなくてはならない。

ポイント

• 符号無し整数の場合
  • $2^n$倍する場合、左に$n$ビットシフトさせて、空いたビットに0 を入れればよい。
  • $2^{-n}$倍する場合、右に$n$ビットシフトさせて、空いたビットに0 を入れればよい。
• 符号付き整数の場合
  • $2^n$倍する場合、左に$n$ビットシフトさせて、空いたビットに0を入れればよい。
  • $2^{-n}$倍する場合、右に$n$ビットシフトさせて、空いたビットには符号ビッ トを入れればよい。

2.2.2 端数の処理

CASL IIの整数をビットシフトを用いて2で割ったりすると、端数(小数部)が生じる。この 端数は、16ビットを越えるので、無視される。ここで、商が切り上げなのか切り下げなの か、疑問が発生する。これについても、実際の整数で考える。

$(5)_{10}$と$(-5)_{10}$を1ビット右にシフトさせて、1/2倍してみる。

$$(5)_{10} \rightarrow(0000\; 0000\; 0000\; 0101)$$

$$\rightarrow(0000\; 0000\; 0000\; 0010)\rightarrow(2)_{10}$$

$$(-5)_{10} \rightarrow(1111\; 1111\; 1111\; 1011)$$

$$\rightarrow(1111\;1111\; 1111\; 1101)\rightarrow(-3)_{10}$$

この結果から、以下のようにまとめることができる。

ポイント

• 正の整数の場合、端数は切り下げとなる。
• 負の整数の場合、端数は切り上げとなる。

ホームページ: Yamamoto's laboratory
著者: 山本昌志