2 問題
2.1 CR発振回路
3年生の実験実習の「発振回路」では、図1の回路の実験を行った。こ こでは、この回路が、本当に発振するか否か、シミュレーションする。ただし、この回路のままだと、計算が大変なので、トランジスターをhパラメーターを用 いて表現する。それは、図2のようになる。これを、1周にわたっ て閉回路の電位差を足しあわせるとゼロになるというキルヒホッフの第2法則を表現しやす いように表したものが図3である。それぞれの図の回路は全く同じであ ることに注意せよ。
2.2 微分方程式
キルヒホッフの法則より、図3の回路では、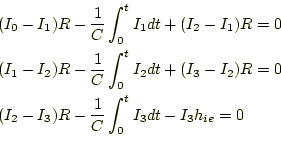 |
が成り立つ。言うまでもないが、回路の電流
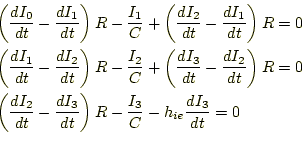 |
となる。このままだと、式が3個で未知数が4個なので、解くことができない。ここで、ト ランジスターのhパラメーターを導入する。トランジスターの特性より
| (3) |
となる。すると、解くべき式は、
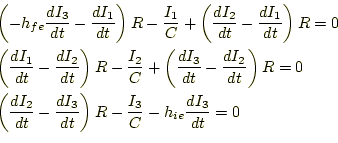 |
である。これが、回路の電流を表す微分方程式である。
これらの連立の微分方程式を4次のルンゲクッタ法で計算すれば良いのであるが、もう少
し変形する必要がある。
![]() のような、形にする。これは、連立方程式な
ので、変形は面倒であるが可能である。計算し易いように変形2すると
のような、形にする。これは、連立方程式な
ので、変形は面倒であるが可能である。計算し易いように変形2すると
となる。
2.3 計算条件
常微分方程式を以下の条件で計算せよ。トランジスターの特性については、私は素人で全 く知らないので、適当に仮定している。それでも、発振の基本的なメカニズムは分かるで あろう。- 計算を簡単にするために
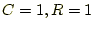 とせよ。また、トランジスターの入力インピー
ダンスは小さいので、
とせよ。また、トランジスターの入力インピー
ダンスは小さいので、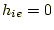 とせよ。増幅率は、
とせよ。増幅率は、
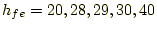 のおの
おので計算し、
のおの
おので計算し、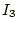 の電流をグラフにせよ。なにが起きているか?。周波数は、
付録の理論計算と合っているか?。
の電流をグラフにせよ。なにが起きているか?。周波数は、
付録の理論計算と合っているか?。
- 先の計算が終われば、増幅率が電流
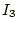 の関数である場合について、考察する。一
般に、トランジスターは電流が増加すると増幅率は下がる。このことにより、発
信の成長が止まり、振幅が一定になる。増幅率が
の関数である場合について、考察する。一
般に、トランジスターは電流が増加すると増幅率は下がる。このことにより、発
信の成長が止まり、振幅が一定になる。増幅率が
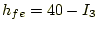
(6)
とした場合(図4)について計算せよ。この場合は、うまく発振しない。なぜか? - 次に、増幅率が
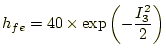
(7)
の場合(図5)について、計算してみよう。この場合は、安定に発振する。なぜか?。安定 状態の波形は正弦波になっているだろうか?。なぜ、そのような波形になるか、考 えてみよう。
これを計算する場合のヒントを与えておく。発振の成長は、種信号の増幅の繰り返しであ
る。実際の発振器の種信号は、熱雑音であったり、スイッチのON/OFFのノイズであったり
する。計算機でシミュレーションする場合、それは、![]() または
または![]() 、
、![]() のいずれかの一つに非常に小さい値を与えれば良い。そして、残りの2つは、ゼロとして
おく。
のいずれかの一つに非常に小さい値を与えれば良い。そして、残りの2つは、ゼロとして
おく。
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成16年10月27日
![\includegraphics[keepaspectratio, scale=1.2]{figure/CR_osc_0.eps}](img1.png)
![\includegraphics[keepaspectratio, scale=1.2]{figure/CR_osc_1.eps}](img2.png)
![\includegraphics[keepaspectratio, scale=1.2]{figure/CR_osc_2.eps}](img3.png)
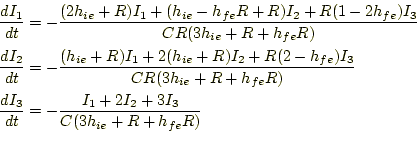
![\includegraphics[keepaspectratio, scale=0.85]{figure/linear_amp.eps}](img17.png)
![\includegraphics[keepaspectratio, scale=0.85]{figure/gauss_amp.eps}](img18.png)