2 方程式
2.1 コンデンサーの性質
コンデンサーを規定する重要な性質にキャパシタンス(静電容量)があるのは、十分承知し ていると思う。これを計算する方法は、いろいろある。その中で、私が好んで使う方法は、 エネルギーから計算する方法である。これは、電場の状態がキャパシタンスを決めるとい う意味で非常に物理的意味が分かりやすい。空間に電場となる。
また、よく知られているように、コンデンサーの電圧![]() とキャパシタンス
とキャパシタンス![]() 、
そして、そこにたまっているエネルギーの関係は、
、
そして、そこにたまっているエネルギーの関係は、
である。コンデンサー内部では、それらは図1のような関係になっ ている。これからも分かるように、コンデンサーの内部には式 (1)が示す静電場のエネルギーが蓄えられている。一方、電 気的には、式2が示すエネルギーが蓄えられている。 これらのエネルギーは、当然等しいので、
という関係がある。この式の左辺の電場はいろいろな方法で計算でき、静電場のエネル ギーを求めることができる。一方、電圧
いままで、よく分からなかった静電容量というものは、コンデンサーに蓄えられるエネルギーを示す 指数と考えて良い。私は、この考え方が好きである。なにしろ、分かりやすい。
2.2 コンデンサー内部の電場
先に示したとおり、コンデンサー内部の電場が分かれば、そのキャパシタンスを求めるこ とができる。それは簡単ではないか、電圧
誘電率が、3次元(![]() の関数)で変化すると計算が大変なので、1次元問題に限ること
にする。2次元や3次元も考え方は同じであるが、計算は大変である。ここで、計算するコ
ンデンサー内部は、図2のとおりとする。誘電率は、座標の関数で、
変化するものとする。
の関数)で変化すると計算が大変なので、1次元問題に限ること
にする。2次元や3次元も考え方は同じであるが、計算は大変である。ここで、計算するコ
ンデンサー内部は、図2のとおりとする。誘電率は、座標の関数で、
変化するものとする。
このような場合の電場はどうなるのであろうか?。一つの方法は、ポアッソン方程式 2
| (4) |
を解くことである。ここで、はポテンシャルで、電圧のことである。少し気取って 書いているのである。この微分方程式を
ポアッソン方程式の代わりに、コンデンサー内部の電場は、そのエネルギーが最小になる
ように分布すると言う原理を使う。当然、このばあいでも、境界条件
![]() は課せられている。コンデンサーの内部のエネルギーは、1次元
なので、
は課せられている。コンデンサーの内部のエネルギーは、1次元
なので、
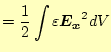 |
||
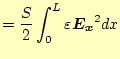 |
(5) |
と書ける。
このポテンシャル分布をコンピューターに計算させるために、コンデンサーの内部を細か くN等分に区切る。この様子を図3に示す。すると、エネルギーは
となる。
静電場のエネルギーが最小になるためには、微分がゼロになる必要がある。このエネルギー
をポテンシャル![]() で微分すると
で微分すると
![$\displaystyle \if 11 \frac{\partial U_s}{\partial \phi_i} \else \frac{\partial^...
...2} \left(\frac{\phi_{i+1}-\phi_{i}}{h}\right) \right]\qquad(i=1,2,3,\cdots,N-1)$](img28.png) |
(7) |
となる。
となる。要するに、この連立1次方程式を計算すれば、任意の誘電率の場合のコンデンサー内部のポテ ンシャル(電圧)が得られる。ポテンシャルが分かれば、電場が分かり、そうすると内部の エネルギーが計算できる。従って、静電容量が求められるわけである。
じつは、ここで示した計算方法は有限要素法と呼ばれている。
- ...このような場合の電場はどうなるのであろうか?。一つの方法は、ポアッソン方程式 2
-
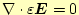 と
と
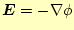 から求められる。
から求められる。
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成16年12月22日
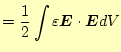
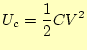
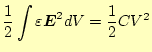
![\includegraphics[keepaspectratio, scale=0.8]{figure/capcitance.eps}](img12.png)
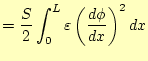
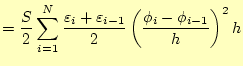
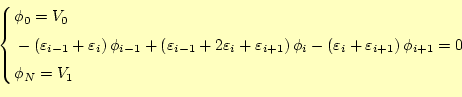
![\includegraphics[keepaspectratio, scale=0.8]{figure/in_capa.eps}](img34.png)
![\includegraphics[keepaspectratio, scale=0.8]{figure/finite.eps}](img35.png)