2 実際のプログラム(手取り足取り)
ここでは、実際のプログラムを作成するときの考え方を示す。最初に、 何にも考えていないガウス・ジョルダン法から出発し、少しずつ機能を追加し て、最終的にパッケージとして完成した関数を作成する事にする。以下の順序でプロ グラムをブラッシュアップする。-
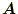 を単位行列にする。そして、
を単位行列にする。そして、
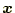 を求める。
を求める。
- 行を交換するだけのピボット選択(部分選択)の機能を追加する。
- 逆行列を計算するルーチンを追加する。
- 不要な配列を排除して、メモリー効率を上げる改造をする。
2.1 素朴なガウス・ジョルダン法(行列の対角化のみ)
まずは、行列の対角化のみのプログラムを作成する。これにより、この節のプログラムは、ピボット選択がないため、実用上問題を含んているが、最初の学 習としてこれは気にしないことにする。ガウス・ジョルダン法のプログラムの学習は簡単 な方が良い。皆さんが、学習ではなく実際に使うプログラムを組むときはピボット選択は 必要不可欠と考えなくてはならない。
さらに、このプログラムは行列が特異な場合でも、計算を続行しようする。その場合、ゼ ロで割ることが生じますので、実行時エラーが発生するであろう。
2.1.1 最外殻のループ
for(ipv=1 ; ipv <= n ; ipv++){
対角化の処理
}
ここで、ipvは対角化する要素
2.1.2 対角成分を1に(ピボット行の処理)
次の処理は、対角成分を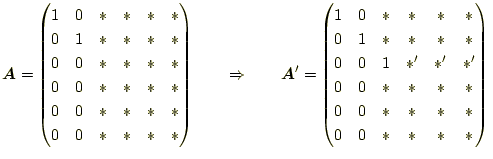 |
と変形したいのである。係数行列
数学では、対角成分を1にするために、その行を対角成分で割る。しかし、
コンピューターのプログラムでは予め逆数を計算して、それを乗じた方が良い。コン
ピューターは除算よりも乗算の方が得意なので効率が良いためである。非同次項
![]() の演算は1回ですが、係数行列
の演算は1回ですが、係数行列
![]() は列毎なので
は列毎なので![]() 回の演算が必
要になる。対角成分を1にする処理は、次のようにする。
回の演算が必
要になる。対角成分を1にする処理は、次のようにする。
inv_pivot = 1.0/a[ipv][ipv];
for(j=1 ; j <= n ; j++){
a[ipv][j] *= inv_pivot;
}
b[ipv] *= inv_pivot;
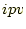 行の
行の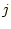 列、
列、
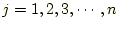 を処理するために、for文を用い
たループになっている。
を処理するために、for文を用い
たループになっている。
- a[ipv][j]
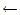 inv_pivot*a[ipv][j]を、通常、C言語では
a[ipv][j] *= inv_pivotと書く。あるいは、a[ipv][j] =
inv_pivot*a[ipv][j]と書いても良い。前者の方が少しかっこいい。
inv_pivot*a[ipv][j]を、通常、C言語では
a[ipv][j] *= inv_pivotと書く。あるいは、a[ipv][j] =
inv_pivot*a[ipv][j]と書いても良い。前者の方が少しかっこいい。
2.1.3 ピボットのある列を0に(ピボット行以外の行の処理)
次は、ピボットがある行以外の処理である。それは、ピボットがある列を全てゼ ロにすることに他ならない。要するに次のように、係数行列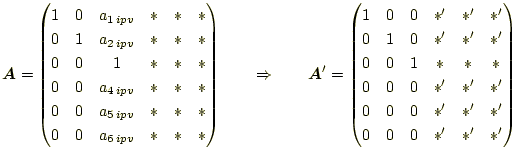 |
このように係数行列
このように変形するのは簡単である。例えば、![]() 行を処理する場合を考える。
行を処理する場合を考える。
![]() 行を、ピボットのある
行を、ピボットのある![]() 行を
行を
![]() 倍したもので引けば良いのである。
倍したもので引けば良いのである。
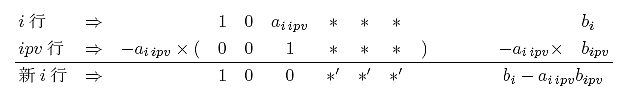 この処理の実際のプログラムは次のようになる。これで、
この処理の実際のプログラムは次のようになる。これで、
![]() 行
行
![]() の全ての
の全ての
![]() の成分を処理をする。
の成分を処理をする。
for(i=1 ; i<=n ; i++){
if(i != ipv){
temp = a[i][ipv];
for(j=1 ; j<=n ; j++){
a[i][j] -= temp*a[ipv][j];
}
b[i] -= temp*b[ipv];
}
}
- 2つのfor文で
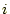 行
行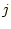 列を処理する。
列を処理する。
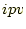 行は対角成分を1にすることで処理が済んでいるので、この行は処理
をしてはならない。そこで、if文を用いて
行は対角成分を1にすることで処理が済んでいるので、この行は処理
をしてはならない。そこで、if文を用いて
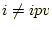 の時、列の
処理をするルーチンが実行されるようになっている。
の時、列の
処理をするルーチンが実行されるようになっている。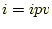 の時は、この処理を
行わないのである。
の時は、この処理を
行わないのである。
これで対角化の処理はおしまい。
2.1.4 素朴なガウス・ジョルダン法のソースプログラム
以上をまとめると、ピボット選択は無く逆行列も求めないのガウス・ジョルダ ン法が完成する。ここで、ひとつ気が付いてほしいのは解ベクトル
/* ========== ガウスジョルダン法の関数 =================*/
void gauss_jordan(int n, double a[][100], double b[]){
int ipv, i, j;
double inv_pivot, temp;
for(ipv=1 ; ipv <= n ; ipv++){
/* ---- 対角成分=1(ピボット行の処理) ---- */
inv_pivot = 1.0/a[ipv][ipv];
for(j=1 ; j <= n ; j++){
a[ipv][j] *= inv_pivot;
}
b[ipv] *= inv_pivot;
/* ---- ピボット列=0(ピボット行以外の処理) ---- */
for(i=1 ; i<=n ; i++){
if(i != ipv){
temp = a[i][ipv];
for(j=1 ; j<=n ; j++){
a[i][j] -= temp*a[ipv][j];
}
b[i] -= temp*b[ipv];
}
}
}
}
2.2 ピボット選択機能追加(行交換)
先ほどの素朴なガウス・ジョルダン法は、爆弾を抱えた関数になっている。もし、対角成 分にゼロが現れたら、ゼロで割ることになり処理が破綻するのである。そこで、それを解 決するピボット選択が登場するのである。もっとも、この問題の解決ばかりでなく、解の 精度も向上する。ピボット選択、ここでは行の交換のみの部分選択を考える。その処理は、
- ピボット列で、最大の値を探す。
- 最大の値のある行をピボット行と交換する。
2.2.1 最大値探索
行交換のみを行う部分選択の場合、ピボットはピボット行以下の最大値とする。これは、 今まで処理した、対角成分が1になっている部分を崩さないためである。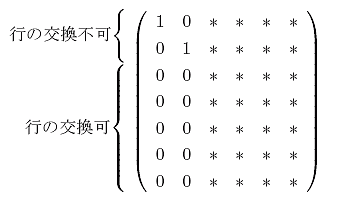 最大値は、
最大値は、ここで、もし最大値がゼロの場合、行列は特異(行列式がゼロ)ということにな り、解は一意的に決まらない。その場合、関数の値としてゼロを返し、その ことをコールした側に伝えるのが良い。
big=0.0;
for(i=ipv ; i<=n ; i++){
if(fabs(a[i][ipv]) > big){
big = fabs(a[i][ipv]);
pivot_row = i;
}
}
if(big == 0.0){return(0);}
row[ipv] = pivot_row;
このプログラムは、以下のことを行っている。
- bigにその列の絶対値の最大が入る。
- 最大値(新しいピボット)がある行は、pivot_rowである。
- ピボットがゼロの場合、行列は特異となる。その場合、処理を中断して、 呼び出し側にゼロを返す。行列が正則な場合、1を返すことにするが、これはこの 関数の最後に書きく。
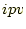 番目に最大値になった行を、配列row[ipv]に入れる。
これは、後で使うことにする。
番目に最大値になった行を、配列row[ipv]に入れる。
これは、後で使うことにする。
2.2.2 行の交換
ピボットとすべき値がある行(pivot_row)がわかったので、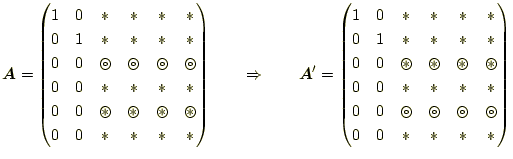 |
入れ替えは、係数行列
ただし、もともと最大の値が![]() 行にある場合は、行の入れ替えは行わない。
行にある場合は、行の入れ替えは行わない。
if(ipv != pivot_row){
for(i=1 ; i<=n ; i++){
temp = a[ipv][i];
a[ipv][i] = a[pivot_row][i];
a[pivot_row][i] = temp;
}
temp = b[ipv];
b[ipv] = b[pivot_row];
b[pivot_row] = temp;
}
2.2.3 部分ピボット選択付きガウス・ジョルダン法のソースプログ
ラム
この![[*]](crossref.png) 節をまとめ、
節をまとめ、
![[*]](crossref.png) 節の素朴なガウス・ジョルダン法とあわせ
ると、部分ピボット選択付きのガウス・ジョルダン法が完成する。
節の素朴なガウス・ジョルダン法とあわせ
ると、部分ピボット選択付きのガウス・ジョルダン法が完成する。
/* ========= ガウスジョルダン法の関数====================== */
int gauss_jordan(int n, double a[][MAXN+10], double b[]){
int ipv, i, j;
double inv_pivot, temp;
double big;
int pivot_row, row[MAXN+10];
for(ipv=1 ; ipv <= n ; ipv++){
/* ---- 最大値探索 ---------------------------- */
big=0.0;
for(i=ipv ; i<=n ; i++){
if(fabs(a[i][ipv]) > big){
big = fabs(a[i][ipv]);
pivot_row = i;
}
}
if(big == 0.0){return(0);}
row[ipv] = pivot_row;
/* ---- 行の入れ替え -------------------------- */
if(ipv != pivot_row){
for(i=1 ; i<=n ; i++){
temp = a[ipv][i];
a[ipv][i] = a[pivot_row][i];
a[pivot_row][i] = temp;
}
temp = b[ipv];
b[ipv] = b[pivot_row];
b[pivot_row] = temp;
}
/* ---- 対角成分=1(ピボット行の処理) ---------- */
inv_pivot = 1.0/a[ipv][ipv];
for(j=1 ; j <= n ; j++){
a[ipv][j] *= inv_pivot;
}
b[ipv] *= inv_pivot;
/* ---- ピボット列=0(ピボット行以外の処理) ---- */
for(i=1 ; i<=n ; i++){
if(i != ipv){
temp = a[i][ipv];
for(j=1 ; j<=n ; j++){
a[i][j] -= temp*a[ipv][j];
}
b[i] -= temp*b[ipv];
}
}
}
return(1);
}
2.3 逆行列計算ルーチンの追加
逆行列を計算するルーチンの追加は難しそうではあるが、実はたんじゅんである。単位行 列を、係数行列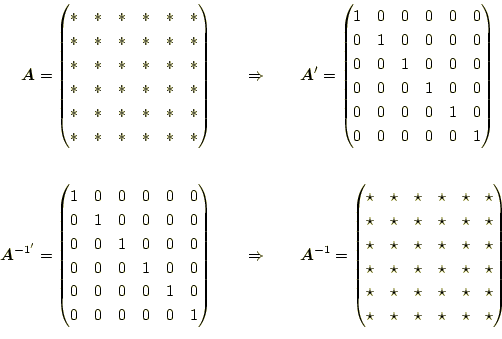 |
これを実現するためには、以下の2つのことをすればよいだけである。
- 単位行列を作成する。
- 作成された単位行列を、係数行列
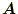 を同じ操作をする。
を同じ操作をする。
2.3.1 単位行列の作成
まず、単位行列を作成する。これは、以下のようにすればよいであろう。
for(i=1 ; i<=n ; i++){
for(j=1 ; j<=n ; j++){
if(i == j){
inv_a[i][j]=1.0;
}else{
inv_a[i][j]=0.0;
}
}
}
2.3.2 逆行列の計算
単位行列inv_aができたので、これを係数行列![[*]](crossref.png) 節のプログラムを以下のように書き換える。
節のプログラムを以下のように書き換える。
- 部分ピボット選択で係数行列の行の交換を行ったならば、同じように
inv_aも行の交換を行う。この部分の処理を
temp = a[ipv][i]; a[ipv][i] = a[pivot_row][i]; a[pivot_row][i] = temp; temp = inv_a[ipv][i]; /* -- これ追加 -- */ inv_a[ipv][i] = inv_a[pivot_row][i]; /* -- これ追加 -- */ inv_a[pivot_row][i] = temp; /* -- これ追加 -- */
と書き換えます。 - 対角成分を1にするためにピボット行をピボットの値で割るところでは、
同じ値で割る。これも、
a[ipv][j] *= inv_pivot; inv_a[ipv][j] *= inv_pivot; /* -- これ追加 -- */
と書き換える。 - ピボット行以外のピボット列を0にするために、ピボット行の定数倍を
引くところでも同じ操作をする。これも、
a[i][j] -= temp*a[ipv][j]; inv_a[i][j] -= temp*inv_a[ipv][j]; /* -- これ追加 -- */
と書き換える。
2.3.3 逆行列計算付きガウス・ジョルダン法のソースプログラム
いままで述べたことを全て網羅したガウス・ジョルダン法の計算の関数は、次 のようになる。
/* ========= ガウスジョルダン法の関数====================== */
int gauss_jordan(int n, double a[][MAXN+10], double b[],
double inv_a[][MAXN+10]){
int ipv, i, j;
double inv_pivot, temp;
double big;
int pivot_row, row[MAXN+10];
/* ---- 単位行列作成 ---------------------------- */
for(i=1 ; i<=n ; i++){
for(j=1 ; j<=n ; j++){
if(i==j){
inv_a[i][j]=1.0;
}else{
inv_a[i][j]=0.0;
}
}
}
for(ipv=1 ; ipv <= n ; ipv++){
/* ---- 最大値探索 ---------------------------- */
big=0.0;
for(i=ipv ; i<=n ; i++){
if(fabs(a[i][ipv]) > big){
big = fabs(a[i][ipv]);
pivot_row = i;
}
}
if(big == 0.0){return(0);}
row[ipv] = pivot_row;
/* ---- 行の入れ替え -------------------------- */
if(ipv != pivot_row){
for(i=1 ; i<=n ; i++){
temp = a[ipv][i];
a[ipv][i] = a[pivot_row][i];
a[pivot_row][i] = temp;
temp = inv_a[ipv][i];
inv_a[ipv][i] = inv_a[pivot_row][i];
inv_a[pivot_row][i] = temp;
}
temp = b[ipv];
b[ipv] = b[pivot_row];
b[pivot_row] = temp;
}
/* ---- 対角成分=1(ピボット行の処理) ---------- */
inv_pivot = 1.0/a[ipv][ipv];
for(j=1 ; j <= n ; j++){
a[ipv][j] *= inv_pivot;
inv_a[ipv][j] *= inv_pivot;
}
b[ipv] *= inv_pivot;
/* ---- ピボット列=0(ピボット行以外の処理) ---- */
for(i=1 ; i<=n ; i++){
if(i != ipv){
temp = a[i][ipv];
for(j=1 ; j<=n ; j++){
a[i][j] -= temp*a[ipv][j];
inv_a[i][j] -= temp*inv_a[ipv][j];
}
b[i] -= temp*b[ipv];
}
}
}
return(1);
}
2.4 メモリー、計算効率の改善
昔、といってもそんなに過去のことではない。プログラマーは出来るだ けメモリーを大事に使った。当時、使えるメモリーが限られていたので、 その資源を有効に活用しなくてはならなかった。いまでこそ、パソコンで1G Byteのメモリーを使うのは何でもないが、たった10年ほど前のメインフ レームと言われた大型のコンピューターでさえ、1つのプログラムが使える領 域は10M Byte程度であった。メモリーと合わせて、計算効率も重要であった。大規模な計算になると、計算が 終了するまで何日も費やす場合がある。そのような場合、プログラムの改 良により、速度が10%アップするとかなりのメリットがあるのである。
そこで、ここではメモリーの効率的な利用を考える。ただし、ここは少し難しい。
2.4.1 メモリーと計算の効率化
これまでの計算過程を考える。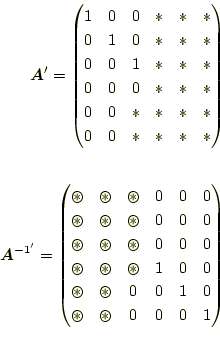 |
となっているはずである。この状態は、
![[*]](crossref.png) 節の
i=4,ipv=3が完了したときである。この行列を良く見ると、係数行列
節の
i=4,ipv=3が完了したときである。この行列を良く見ると、係数行列
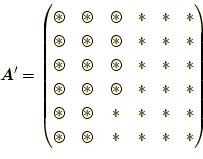 |
としたくなる。そうすると、メモリーが半分で済む。これは、
これを実現するのは、簡単である。次のようにプログラムを書けばよい。
/* ---- 対角成分=1(ピボット行の処理) ---------- */
inv_pivot = 1.0/a[ipv][ipv];
a[ipv][ipv]=1.0; /* --- この行を追加 --- */
for(j=1 ; j <= n ; j++){
a[ipv][j] *= inv_pivot;
}
b[ipv] *= inv_pivot;
/* ---- ピボット列=0(ピボット行以外の処理) ---- */
for(i=1 ; i<=n ; i++){
if(i != ipv){
temp = a[i][ipv];
a[i][ipv]=0.0; /* --- この行を追加 --- */
for(j=1 ; j<=n ; j++){
a[i][j] -= temp*a[ipv][j];
}
b[i] -= temp*b[ipv];
}
}
このようにすると必要なメモリーは、![[*]](crossref.png) 節のプログラ
ムに比べて半分になる。さらに、計算時間も半分になる。
節のプログラ
ムに比べて半分になる。さらに、計算時間も半分になる。
![[*]](crossref.png) 節では、計算結果が0や
節では、計算結果が0や![]() の場合も計算し
ていたが、このプログラムではそれを省いている。
の場合も計算し
ていたが、このプログラムではそれを省いている。
2.4.2 逆行列の列の入れ替え
これで、メモリーと計算の効率化が図れたが、このままでは
当然、
![]() の逆行列ということは、乗算すると下のように単位行列になる。
の逆行列ということは、乗算すると下のように単位行列になる。
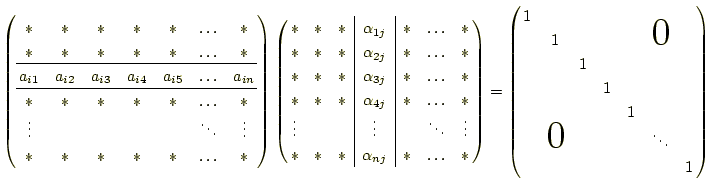 |
すなわち、元の行列の行ベクトルと逆行列の列ベクトルの内積が、
| (元の行列の |
という関係を満たしていることを意味する。
このようなわけで、元の行列の行を入れ替えた場合、その逆行列は元の行列の逆行列の列 を入れ替えたものになる。従って、ピボット選択により係数行列の行を入れ替えると、逆 行列の列を入れ替える必要が生じる。実際にプログラムでは、以下のようにする。
/* ---- 列の入れ替え(逆行列) -------------------------- */
for(j=n ; j>=1 ; j--){
if(j != row[j]){
for(i=1 ; i<=n ; i++){
temp = a[i][j];
a[i][j]=a[i][row[j]];
a[i][row[j]]=temp;
}
}
}
2.4.3 効率化したガウス・ジョルダン法のソースプログラム
これで、ほとんどガウス・ジョルダン法の計算の関数は、完成である。この関数 は、かなり実用に使えるであろう。残っている問題は、- 列交換による完全ピボット選択の改良。これはそんなに難しくない。
- 丸め誤差を考慮した特異行列の判定。これは大変難しい。
これ以上、改良するのは大変なので、ほとんど問題なく使える関数のプログラ ムを以下に示す。
/* ========= ガウスジョルダン法の関数====================== */
int gauss_jordan(int n, double a[][MAXN+10], double b[]){
int ipv, i, j;
double inv_pivot, temp;
double big;
int pivot_row, row[MAXN+10];
for(ipv=1 ; ipv <= n ; ipv++){
/* ---- 最大値探索 ---------------------------- */
big=0.0;
for(i=ipv ; i<=n ; i++){
if(fabs(a[i][ipv]) > big){
big = fabs(a[i][ipv]);
pivot_row = i;
}
}
if(big == 0.0){return(0);}
row[ipv] = pivot_row;
/* ---- 行の入れ替え -------------------------- */
if(ipv != pivot_row){
for(i=1 ; i<=n ; i++){
temp = a[ipv][i];
a[ipv][i] = a[pivot_row][i];
a[pivot_row][i] = temp;
}
temp = b[ipv];
b[ipv] = b[pivot_row];
b[pivot_row] = temp;
}
/* ---- 対角成分=1(ピボット行の処理) ---------- */
inv_pivot = 1.0/a[ipv][ipv];
a[ipv][ipv]=1.0;
for(j=1 ; j <= n ; j++){
a[ipv][j] *= inv_pivot;
}
b[ipv] *= inv_pivot;
/* ---- ピボット列=0(ピボット行以外の処理) ---- */
for(i=1 ; i<=n ; i++){
if(i != ipv){
temp = a[i][ipv];
a[i][ipv]=0.0;
for(j=1 ; j<=n ; j++){
a[i][j] -= temp*a[ipv][j];
}
b[i] -= temp*b[ipv];
}
}
}
/* ---- 列の入れ替え(逆行列) -------------------------- */
for(j=n ; j>=1 ; j--){
if(j != row[j]){
for(i=1 ; i<=n ; i++){
temp = a[i][j];
a[i][j]=a[i][row[j]];
a[i][row[j]]=temp;
}
}
}
return(1);
}
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成16年11月17日