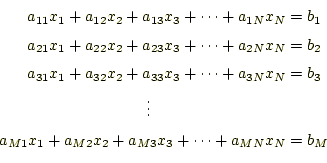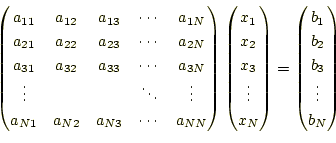1 連立方程式
1.1 表現方法
言うまでも無く連立1次方程式(Linear Equations)は、次のような形をしている。ここでは、
式(1)は行列とベクトルで書くと、式がすっきりして 考えやすくなる。書き直すと、
となるのは、以前学習したとおりである。それぞれの行列とベクトルは、
 |
を表す。行列は大文字の太文字(bold)スタイル、ベクトルは小文字 の太文字スタイル、それぞれの成分は標準スタイルで表されることが多い。
ここで、解く問題は行列
![]() が
が
![]() の正方行列で、その行列式が
ゼロでないものとする。要するに、普通に解ける連立方程式である。ここで、
解くべき問題は、既知の
の正方行列で、その行列式が
ゼロでないものとする。要するに、普通に解ける連立方程式である。ここで、
解くべき問題は、既知の
![]() と
と
![]() から、行列方程式(
から、行列方程式(![[*]](crossref.png) )を満たす、
)を満たす、
![]() を求めることになる。この行列方
程式解く過程で、
を求めることになる。この行列方
程式解く過程で、
![]() の逆行列や行列式の値を求めることができる。逆
行列や行列式は連立方程式と密接にかかわっているのである。
の逆行列や行列式の値を求めることができる。逆
行列や行列式は連立方程式と密接にかかわっているのである。
通常、連立1次方程式(1)は
と書き表せる。このようにすると、見通しがかなり良くなる。皆さんも、 今後連立方程式を書くときは、行列とベクトルで書く方が良いであろう。 ちょっとばかり格好良い。
行列やベクトルを使うと、格好良いばかりでなくコンピューターで扱いやすく
なる。例えば、行列
![]() の要素
の要素![]() はプログラム中では2次元配
列a[i][j]として扱える。同様にベクトル
はプログラム中では2次元配
列a[i][j]として扱える。同様にベクトル![]() は1次元配列
b[k]として扱える。
は1次元配列
b[k]として扱える。
1.2 計算方法
連立1次方程式は、クラメールの公式により、解のベクトル |
(5) |
である。これは、2つの行列式を計算する必要があり、計算量 が大変多くなる。したがって、
次に考えられるのは、
![]() の逆行列
の逆行列
![]() を用いて、
を用いて、
![]() から計算する方法である。この方法も、計算量と精
度の面で問題がある。
から計算する方法である。この方法も、計算量と精
度の面で問題がある。
連立1次方程式の計算方法は大別して、2通りある。1つは、ここで学習す
る消去法で、他方は反復法と言われる方法である。どちらが良いかは、係数行列
![]() の性質に依存する。一般に、
の性質に依存する。一般に、
![]() が密なとき、即ちほとんどの要
素がゼロでないときは、消去法が有利である。一方、殆どの要素が
ゼロで、
が密なとき、即ちほとんどの要
素がゼロでないときは、消去法が有利である。一方、殆どの要素が
ゼロで、
![]() が疎のとき、反復法が有利である。
が疎のとき、反復法が有利である。
ここでは消去法を学習するが、反復法について簡単に紹介しておく。まず、
係数行列を
![]() と変形します。すると、元の連立1次方程
式は、
と変形します。すると、元の連立1次方程
式は、
![]() となる。これを解くために、
漸化式
となる。これを解くために、
漸化式
![]() とする。もし、
初期値
とする。もし、
初期値
![]() が良ければ、
が良ければ、
![]() は真の解
は真の解
![]() に
収束する。もちろん、
に
収束する。もちろん、
![]() は容易に計算できる連立1次方程式になるよ
うに選ぶ。この選び方により、ヤコビの反復法やガウス・ザイデル法、
SOR法などがある。
は容易に計算できる連立1次方程式になるよ
うに選ぶ。この選び方により、ヤコビの反復法やガウス・ザイデル法、
SOR法などがある。
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成16年11月9日