2 非線型方程式の複素数解

2.1 実数解の場合

複素数に進む前に実数のニュートン法の復習を行う。以前配布(7月1日)したプ リントでは、図によるニュートン法の説明を行い、漸化式を示した。ここでは、 別のアプローチを行う。別のアプローチであるが、その根本精神は同じで、

• 解に近いところでは、直線で近似できる²。

ということである。

では、異なったアプローチで漸化式を求める。いつものように、$f(x)=0$の方 程式の解を$x=\alpha$とする。即ち、 $f(\alpha)=0$である。そして、$i$番目 の近似解を$x_i$とする。ここから、$\Delta x$だけ移動したところの値は、

$$\begin{aligned}f(x_i+\Delta x)&=f(x_i) +f^\prime(x_i)\Delta x +... ... x^2 +\cdots\\ &\simeq f(x_i)+f^\prime(x_i)\Delta x \end{aligned}$$

となる。もし、 $f(x_i+\Delta x)=0$、即ち、 $\alpha=x_i+\Delta x$となるよ うに、$\Delta x$を選ぶことができたら、解の計算は簡単である。この場合、 式(2)の最後の式から、

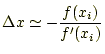$$\Delta x \simeq -\frac{f(x_i)}{f^\prime(x_i)}$$ (2)

となる。したがって、 $\alpha=x_i+\Delta x$から、次の近似解は

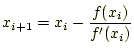$$x_{i+1}=x_i-\frac{f(x_i)}{f^\prime(x_i)}$$ (3)

となる。前回、図により求めた漸化式と同じである。異なる説明であったが、 内容はまったく同じであることを理解して欲しい。

2.2 複素数解の場合

2.2.1 漸化式

実数とまったく同じ議論が、複素数でも成り立つ。ただし、複素関数で重要な 特異点付近では、この方法は使えない。テイラー級数ではなく、ローラン級数 の$-1$乗よりも小さい項が重要となるからである。実数の場合も、特異点はだ めなのと同じである。

実数とまったく同じ議論より、方程式

$$w(z)=0$$ (4)

の近似解は、漸化式

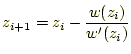$$z_{i+1}=z_i-\frac{w(z_i)}{w^\prime(z_i)}$$ (5)

より求めることができる。この式の算出は、先ほどの実数の場合と全く同じで ある。

前回とは異なり、実数の場合の漸化式をグラフを用いないで説明したのは、複 素数に拡張するためである。複素数のグラフは大変である。

2.2.2 プログラム作成のために

FORTRANと違って、C言語では複素数をそのまま扱うことができない。FORTRAN は複素数をそのまま扱えるのである。これは非常に便利で、いまだに科学技術 計算でFORTRANが現役である大きな理由となっている。一方、C言語の場合、2 つの実数を用いて、複素数を取り扱う。実数部と虚数部である。これは、数学 で学習したように

$$z=x+iy$$ (6)

とすればよい。$x$と$y$を用いるわけである。C言語では、構造体で定義する のが美しいと思われるが、学習していないので、ここではどうでも良い。

同様に関数も

$$w(z)=u(z)+iv(z)$$ (7)

と実数部と虚数部に分けて計算する。
ホームページ: Yamamoto's laboratory
著者: 山本昌志