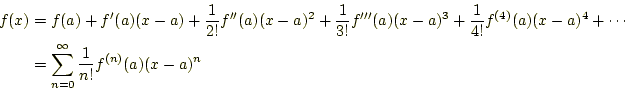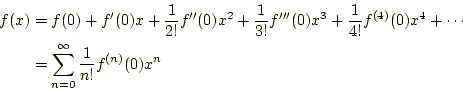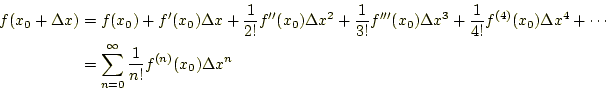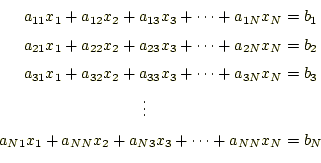1 基本

1.1 テイラー展開

数値計算は言うに及ばず科学技術全般の考察にテイラー展開(Taylor expansion)は、重要な役割を果たす。電気の諸問題を考察する場合、いたるところにテイラー展開は顔を出すので、十分理解しなくてはならない。まずは、

の回りのテイラー展開は、

$\begin{align*}\begin{aligned}f(x)&=f(a)+f^\prime(a)(x-a)+\frac{1}{2!}f^{\prime\p... ...ots\\ &=\sum_{n=0}^\infty\frac{1}{n!}f^{(n)}(a)(x-a)^n \end{aligned}\end{align*}$

(1)

と書ける。0の階乗は

となることに注意。 $f^{(n)}(a)$ は、関数

を

回微分したときの

の値である。テイラー展開は、任意の関数

は、無限のべき級数に展開できると言っている。その係数が、 $\frac{1}{n!}f^{(n)}(a)$ である。次に、

としてみる。この場合、

$\begin{align*}\begin{aligned}f(x)&=f(0)+f^\prime(0)x+\frac{1}{2!}f^{\prime\prime... ...+\cdots\\ &=\sum_{n=0}^\infty\frac{1}{n!}f^{(n)}(0)x^n \end{aligned}\end{align*}$

(2)

となる。これがマクローリン展開(Maclaurin expansion)である。次に $x-a=\Delta x$ とする。そして、

とすると

$\begin{align*}\begin{aligned}f(x_0+\Delta x)&=f(x_0)+f^\prime(x_0)\Delta x +\fra... ... &=\sum_{n=0}^\infty\frac{1}{n!}f^{(n)}(x_0)\Delta x^n \end{aligned}\end{align*}$

(3)

となる。これは、しばしばお目にかかるパターン。

通常我々がテイラー展開を使う場合、この式 (1)～式(3) のいずれかである。

1.2 連立一次方程式の表現

個の未知数があり、それが式の数が等し連立方程式を考える。この場合、連立方程式は

$\begin{equation*}\begin{aligned}a_{11}x_1+a_{12}x_2+a_{13}x_3+\cdots+a_{1N}x_N&=... ...a_{N1}x_1+a_{NN}x_2+a_{N3}x_3+\cdots+a_{NN}x_N&=b_N \end{aligned}\end{equation*}$

と書くのは中学校以来の習慣である。実際の問題を解く場合、これでは見通しが悪いので線形代数の知識を使う。この連立方程式の係数と未知数、非同次項を、

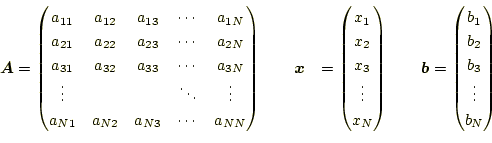$\begin{equation*}\begin{aligned}\boldsymbol{A}&= \begin{pmatrix}a_{11} & a_{12} ... ...rix}b_1 \\ b_2 \\ b_3 \\ \vdots\\ b_N \end{pmatrix} \end{aligned}\end{equation*}$

のような行列やベクトルで表す。すると、連立方程式(4)は、

$\displaystyle \boldsymbol{A}\boldsymbol{x}=\boldsymbol{b}$

(6)

のように表現できる。
ホームページ: Yamamoto's laboratory
著者: 山本昌志

Yamamoto Masashi
平成16年11月29日