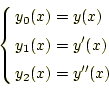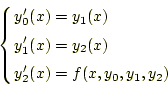2 常微分方程式の数値計算法
数値計算により、近似解を求める微分方程式は、である。これは問題として与えられ、この式に従う
2.1 オイラー法
常微分方程式の解をである。この式の右辺第2項は、式(7) から計算できる。したがって、テイラー展開は、次のように書き表わせる。
| (9) |
オイラー法での数値計算では、計算の刻み幅![]() は十分に小さいとして、
は十分に小さいとして、
| (10) |
を計算する。この場合、計算の精度は1次と言う2。
オイラー法では、次の漸化式に従い数値計算を進める。解である
![]() が同じ手続きで計算できる。
実際にプログラムを行うときは、forやwhileを用いて繰り
返し計算を行い、結果の
が同じ手続きで計算できる。
実際にプログラムを行うときは、forやwhileを用いて繰り
返し計算を行い、結果の![]() と
と![]() は、配列x[i] や
y[i]に格納するのが常套手段である。
は、配列x[i] や
y[i]に格納するのが常套手段である。
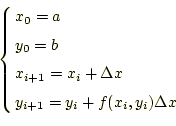 |
この方法の計算のイメージは、図1の通りである。明らか に、出発点の導関数のみ利用しているために精度が悪いことが理解できる。式 も対称でないため、逆から計算すると元に戻らない。
2.2 2次のルンゲクッタ法(ホイン法)
2次のルンゲ・クッタと呼ばれる方法は、いろいろある。ここでは、ホイン法をしめす。
先に示したように、オイラー法の精度は1次であるが、2次のルンゲ・
クッタ法では2次となる。今まで刻み幅を![]() と記述していたが、簡単のため
と記述していたが、簡単のため![]() と
表現する。
と
表現する。
2次の精度ということは、テイラー展開より
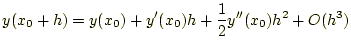 |
(12) |
となっていることを意味する。即ち、計算アルゴリズムが、
となっている。
式(13)から分かるように、![]() の増分
の増分![]() を計算する
ためには、1階微分と2階微分の2項を満たす式が必要である。そうすると少なく
とも、2点の値が必要となる。2点として、計算区間の両端の導関数の値を
使う。この導関数は問題として与えられているので、計算は簡単である。そ
うして、区間の増分を
を計算する
ためには、1階微分と2階微分の2項を満たす式が必要である。そうすると少なく
とも、2点の値が必要となる。2点として、計算区間の両端の導関数の値を
使う。この導関数は問題として与えられているので、計算は簡単である。そ
うして、区間の増分を
![]() をパラメーターとした和で表すことに
する。即ち、以下の通りである。
をパラメーターとした和で表すことに
する。即ち、以下の通りである。
この
| (15) |
となる。これを、式(13)と比較すると、
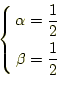 |
とすれば良いことが分かる。これで、必要な式は求まった。まとめる と、式(7)を数値計算で近似解を求める には次式を使うことになる。
この式は、図2のようになる。オイラー法の図 1との比較でも、精度が良いことが分かる。
2.3 4次のルンゲ・クッタ法
今まで示したオイラー法や2次のルンゲ・クッタ法のように、パラメーターを 増やして誤差項の次数を上げていく方法で、最良の方法と言われるのが4次の ルンゲ・クッタ法である。パラメーターを増やして、5, 6, 7,ということで、皆さんが常微分方程式を計算する必要が生じたときは、何はと もあれ4次のルンゲ・クッタで計算すべきである。普通の科学に携わる人にとっ て、4次のルンゲ・クッタは常微分方程式の最初で最後の解法である。
4次のルンゲ・クッタの公式は、式(18)に示す通りである。そし て、これは図3のように表すことができる。
2.4 プログラム(4次のルンゲ・クッタ法)
実際の微分方程式を4次のルンゲ・クッタ法で計算するプログラムを示す。計算結果は、配列「x[]」と 「y[]」に格納される。実際にプログラムでは、この結果を利用してグラフにしたりする のであるが、ここでは計算のみとする。
#include <stdio.h>
#include <math.h>
#define IMAX 100001
double func(double x, double y);
/*================================================================*/
/* main function */
/*================================================================*/
int main(void){
double x[IMAX], y[IMAX];
double final_x, h;
double k1, k2, k3, k4;
int ncal, i;
/*--- set initial condition and cal range ---*/
x[0]=0.0;
y[0]=0.0;
final_x=10.0;
ncal=10000;
/* --- size of calculation step --- */
h=(final_x-x[0])/ncal;
/* --- 4th Runge Kutta Calculation --- */
for(i=0; i < ncal; i++){
k1=h*func(x[i],y[i]);
k2=h*func(x[i]+h/2.0, y[i]+k1/2.0);
k3=h*func(x[i]+h/2.0, y[i]+k2/2.0);
k4=h*func(x[i]+h, y[i]+k3);
x[i+1]=x[i]+h;
y[i+1]=y[i]+1.0/6.0*(k1+2.0*k2+2.0*k3+k4);
}
return 0;
}
/*================================================================*/
/* define function */
/*================================================================*/
double func(double x, double y){
double dydx;
dydx=sin(x)*cos(x)-y*cos(x);
return(dydx);
}
2.5 高階の常微分方程式
2.5.1 1階の連立微分方程式に変換
ここまで示した方法は、1階の常微分方程式しか取り扱えないので不便である。そこで、 高階の常微分方程式を1階の連立微分方程式に直す方法を示す。要するに、高階の常 微分方程式を連立1階常微分方程式に直し、4次のルンゲ・クッタ法を適用すれば良いので ある。例えば、次のような3次の常微分方程式があったする。この3階常微分方程式を次に示す式を用いて変換する。
この式を用いて、式(20)を書き直すと
となる。これで、3階の常微分方程式が3元の1階の連立常微分方程式に変換できた。2階で あろうが4階
2.5.2 練習問題
以下の高次常微分方程式を連立1階微分方程式に書き換えなさい。ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成16年11月29日

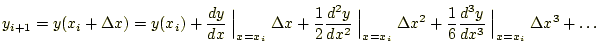
![\includegraphics[keepaspectratio, scale=0.7]{figure/diff_eq/Euler.eps}](img31.png)
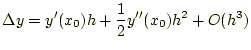
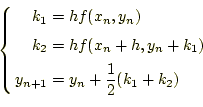
![\includegraphics[keepaspectratio, scale=0.7]{figure/diff_eq/RK2_1.eps}](img41.png)
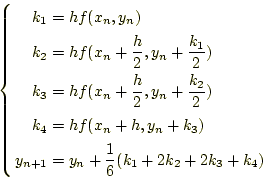
![\includegraphics[keepaspectratio, scale=0.7]{figure/diff_eq/RK4.eps}](img44.png)