2 ベクトル場の回転とストークスの定理
2.1 ベクトル場の回転
2.1.1 大きな領域での話
完全流体の渦の速度は、半径に反比例する。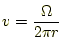 |
(1) |
ここで、
となる。これは、これは渦の中心を取り囲んで、一回りすれば、積分の経路に よらずいつも同じ値をとる。それは、次のように考える。渦の中心を中心に同 心円の積分の値はいつも同じ、
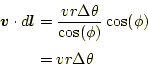 |
となる。したがって、線分1に沿っても、線分2に沿っても積分の値は同じであ る。このことから、どこのパスで積分しても値は同じことが理解できる。
これまでの話は渦であったが、電流と磁場は
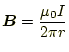 |
(4) |
という関係があるので、同じことが言える。この式の左辺はベクトル、右辺は スカラーになっており矛盾しているが、今は細かいことを考えないこととする。 後で、静磁場を学習するときに矛盾ない式を示すので我慢してほしい。磁場の 式(2)に対応するものは、
となる。
2.1.2 微小領域での話
次に、教科書に従い、微小領域でベクトル場の回転を考える。ただし、教科書 の表現は気に食わないので、少し図2のように変える。積分 は、図の矢印に沿って一周、積分を行う。
まず、図の下の部分と上の部分の積分を考える。ただし、![]() と
と
![]() が非常に小さいので、積分は積の和に置き換えられる。同じx座標
で、上の部分と下の部分の積分は
が非常に小さいので、積分は積の和に置き換えられる。同じx座標
で、上の部分と下の部分の積分は
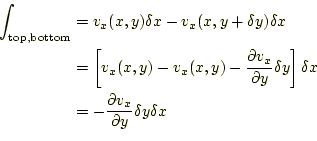 |
となる。テイラー展開の1次まで計算し、2次以降の高次を無視するのは常套手 段でよく覚えておく必要がある。同様に、左右の積分は、
 |
(7) |
となる。この上下の積分と左右の積分を足し合わせて、一周の積分とする。そ れは、
 |
となる。この式の右辺の括弧内は、まさに応用解析で学習したベクトル場の回 転である。すなわち、
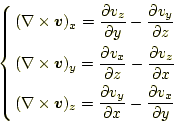 |
である。したがって、微小区間の積分は、
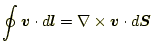 |
(10) |
と書き改めることができる。この積分の値は、微小領域
| (11) |
となる。次に渦の密度
| (12) |
定義する。すると、
| (13) |
という関係が導かれる。要するにベクトル場を微分(
| (14) |
が磁場と電流にもある。ここで
2.1.3 ストークスの定理
先ほどのという関係が得られる。これをストークスの定理という。
このストークスの定理から、
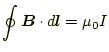 |
(16) |
が得られる。この式が言っていることは、ある閉じた領域で一周にわたり磁場 を積分すれば、電流が分かるということである。
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成16年9月28日
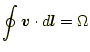
![\includegraphics[keepaspectratio, scale=1.0]{figure/uzu_int.eps}](img14.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/int_rot.eps}](img30.png)
