3 スカラー場の勾配
これまで、ベクトル場の微分として、発散(
![]() の位置から
の位置から
![]() へ移動したときの、山の高さの変化
へ移動したときの、山の高さの変化![]() は、
は、
 |
となる。このときの演算
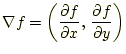 |
(18) |
を勾配と言う。要するにスカラー場にナブラ演算子を作用させること。実際は、 3次元の場合が多く、普通は
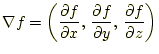 |
(19) |
と書かれる。
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成16年9月28日
![]() の位置から
の位置から
![]() へ移動したときの、山の高さの変化
へ移動したときの、山の高さの変化![]() は、
は、
 |
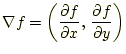 |
(18) |
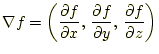 |
(19) |