2 ベクトルの演算

2.1 ベクトルの和と積

これについては、取り立てて、説明することは無いだろう。

2.2 ラプラス演算子

ベクトル演算子同士の内積をとった結果、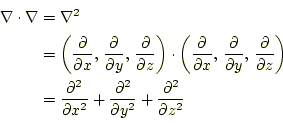

$\begin{equation*}\begin{aligned}\nabla\cdot\nabla &=\nabla^2 &=\left( \frac{\p... ...l^2}{\partial y^2}+ \frac{\partial^2}{\partial z^2} \end{aligned}\end{equation*}$

の新しくできる演算子をラプラス演算子(ラプラシアン)と言う。 $\nabla^2$ の代わりに $\Delta$ と書くこともある。

これは、見て分かるようにスカラー演算子である。スカラー演算子であるため、スカラーやベクトルに作用することができる。スカラー場 $\phi$ に作用すると、次のようなスカラー場ができる。

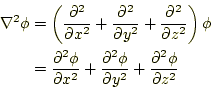$\begin{equation*}\begin{aligned}\nabla^2\phi &=\left( \frac{\partial^2}{\partial... ...\partial y^2}+ \frac{\partial^2 \phi}{\partial z^2} \end{aligned}\end{equation*}$

ベクトル場 $\boldsymbol{h}$ に作用すると、次のようなベクトル場ができる。

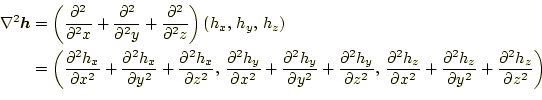$\begin{equation*}\begin{aligned}\nabla^2 \boldsymbol{h} &=\left( \frac{\partial^... ...l y^2}+ \frac{\partial^2 h_z}{\partial z^2} \right) \end{aligned}\end{equation*}$

2.3 ベクトル場の2階微分

以下の計算は、「ファインマン物理学III 電磁気学」の第2章を参考にしている。

2.3.1 便利な公式

ベクトル場の2階微分はいろいろな場面で出くわす。自然科学を学習すると2階微分に非常に多く出くわす。これは、なぜなのだろうか?不思議である。可能なベクトル場の2階微分は、

	$\displaystyle \nabla\cdot(\nabla T)$	(4)
	$\displaystyle \nabla\times(\nabla T)$	(5)
	$\displaystyle \nabla(\nabla\cdot\boldsymbol{h})$	(6)
	$\displaystyle \nabla\cdot(\nabla\times\boldsymbol{h})$	(7)
	$\displaystyle \nabla\times(\nabla\times\boldsymbol{h})$	(8)

である。

ベクトルの微分演算子 $\nabla$ は、通常のベクトルの演算と同じように振舞う。この記号は非常に便利である。したがって、通常のベクトルの演算で0になるものを探し、その関係を利用して式(4)～ (8)の演算で0になるものを類推する。以下のベクトルの演算が0になることは直ちに分かる。

	$\displaystyle \boldsymbol{A}\times(\boldsymbol{A}T)=(\boldsymbol{A}\times\boldsymbol{A})T=0$	(9)
	$\displaystyle \boldsymbol{A}\cdot(\boldsymbol{A}\times\boldsymbol{B})=0$	(10)

これらの関係から、

	$\displaystyle \nabla\times(\nabla T)=0$	(11)
	$\displaystyle \nabla\cdot(\nabla\times\boldsymbol{h})=0$	(12)

と類推できる。類推ではあるが、これは正しい式である。最後の練習問題でこの式が正しいことを確認すること。

次にベクトル公式

$\displaystyle \boldsymbol{A}\times(\boldsymbol{B}\times\boldsymbol{C}) =\boldsy... ...symbol{A}\cdot\boldsymbol{C})-\boldsymbol{C}(\boldsymbol{A}\cdot\boldsymbol{B})$

(13)

を用いた場合を考える。

と

を $\nabla$ で置き換え、 $\boldsymbol{C}$ を $\boldsymbol{h}$ とすると、

$\displaystyle \nabla\times(\nabla\times\boldsymbol{h}) =\nabla(\nabla\cdot\boldsymbol{h})-\boldsymbol{h}(\nabla\cdot\nabla)$

(14)

となる。右辺第2項の $\boldsymbol{h}(\nabla\cdot\nabla)$ が変である。この問題を避けるために、少し技巧的であるが、式(15)を

$\displaystyle \boldsymbol{A}\times(\boldsymbol{B}\times\boldsymbol{C}) =\boldsy... ...symbol{A}\cdot\boldsymbol{C})-(\boldsymbol{A}\cdot\boldsymbol{B})\boldsymbol{C}$

(15)

とすればよい。右辺第2項は、ベクトル $\boldsymbol{C}$ とスカラー $\boldsymbol{A}\cdot\boldsymbol{B}$ との積であるため、演算の順序を入れ替えても良い。こうすると、式(16)は

$\begin{equation*}\begin{aligned}\nabla\times(\nabla\times\boldsymbol{h}) &=\nabl... ...a(\nabla\cdot\boldsymbol{h})-\nabla^2\boldsymbol{h} \end{aligned}\end{equation*}$

となり、正しそうである。事実、これは正しい式である。成分ごとに、きちんと微分を行えば分かる。

以上で、最初に示した2階の微分のうち、式(5)と (7)、(8)の公式を導いた。残りは、特に興味のあるものは無い。そこで、以上の結果をまとめると

	$\displaystyle \nabla\cdot(\nabla T)=\nabla^2T=$ スカラー場	(17)
	$\displaystyle \nabla\times(\nabla T)=0$	(18)
	$\displaystyle \nabla(\nabla\cdot\boldsymbol{h})=$ ベクトル場	(19)
	$\displaystyle \nabla\cdot(\nabla\times\boldsymbol{h})=0$	(20)
	$\displaystyle \nabla\times(\nabla\times\boldsymbol{h}) =\nabla(\nabla\cdot\boldsymbol{h})-\nabla^2\boldsymbol{h}$	(21)
	$\displaystyle (\nabla\cdot\nabla)\boldsymbol{h}=\nabla^2\boldsymbol{h}=$ ベクトル場	(22)