3 ベクトル解析まとめ

3.1 微分

3.1.1 微分演算子

ベクトル解析に使う記号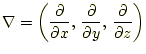$\nabla$は、通常の微分の記号$d$と同様の役割を果 たす。要するに、$\nabla$は微分のことで

$$\nabla=\left( \frac{\partial}{\partial x}, \frac{\partial}{\partial y}, \frac{\partial}{\partial z} \right)$$ (25)

のことである。これは、微分の演算子であるが、これをベクトルとして取り 扱った代数公式は全て成り立つ。非常に興味深いこととともに、便利である。

3.1.2 スカラー場の勾配

このベクトル演算子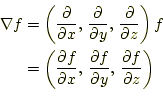$\nabla$を用いた、微分は3つある。ひとつは、勾配と呼 ばれるもので、スカラー場に作用する。

$$\begin{aligned}\nabla f&=\left( \frac{\partial}{\partial x}, ... ...partial y}, \frac{\partial f}{\partial z} \right) \end{aligned}$$

これは、スカラー場$f$に作用して、ベクトル場$\nabla f$を作っている。ス カラー場$f$の傾きを表している。$\nabla f$の代わりに、 $\textrm{grad} f$と書かれる事もある。

3.1.3 ベクトル場の発散

次に、演算子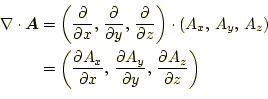$\nabla$とベクトル場 $\boldsymbol{A}$の内積(スカラー積)である。

$$\begin{aligned}\nabla\cdot\boldsymbol{A}&=\left( \frac{\partial... ...rtial y}, \frac{\partial A_z}{\partial z} \right) \end{aligned}$$

ベクトル場 $\boldsymbol{A}$に作用して、スカラー場 $\nabla\cdot\boldsymbol{A}$を作ってい る。この微分は

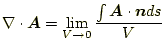$$\nabla\cdot\boldsymbol{A}=\lim_{V \to 0}\frac{\int \boldsymbol{A}\cdot\boldsymbol{n}ds}{V}$$ (28)

と定義され、ベクトル場$A$の発散と呼ばれるスカラー量を導くときに使われ る。発散とは、湧き出しや吸い込みのことである。 $\nabla\cdot\boldsymbol{A}$の代わりに、 $\textrm{div} \boldsymbol{A}$と書かれる事もあ る。

3.1.4 ベクトル場の回転

最後に、演算子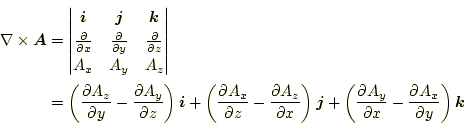$\nabla$とベクトル場 $\boldsymbol{A}$の外積(ベクトル積)である。

$$\begin{aligned}\nabla\times\boldsymbol{A}&= \begin{vmatrix}\bol... ...rac{\partial A_x}{\partial y} \right)\boldsymbol{k} \end{aligned}$$

ベクトル場 $\boldsymbol{A}$に作用して、ベクトル場 $\nabla\times\boldsymbol{A}$を作ってい る。この微分は

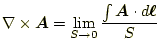$$\nabla\times\boldsymbol{A}=\lim_{S \to 0}\frac{\int \boldsymbol{A}\cdot d\boldsymbol{\ell}}{S}$$ (30)

と定義され、ベクトル場$A$の回転と呼ばれるベクトル量を導くときに使われ る。 $\nabla\times\boldsymbol{A}$の代わりに、 $\textrm{rot} \boldsymbol{A}$や $\textrm{curl} \boldsymbol{A}$と書かれる事もある。

3.2 積分

3.2.1 スカラー場の勾配の線積分

座標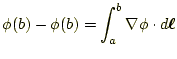$b$から$a$を引いたスカラー場の差は、$a$から$b$までの任意の曲線に沿っ たスカラー場の接線成分の線積分に等しい。

$$\phi(b)-\phi(b)=\int_a^b \nabla\phi\cdot d\boldsymbol{\ell}$$ (31)

3.2.2 ベクトル場の発散の面積分

任意のベクトル場の任意の閉曲面の法線方向成分の面積分は、その面内の発散 の体積分に等しい。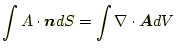

$$\int A\cdot\boldsymbol{n}dS=\int \nabla\cdot\boldsymbol{A}dV$$ (32)

これを、ガウスの定理と言う。

3.2.3 ベクトル場の回転の体積分

任意のベクトル場を任意の閉曲線に沿ってのその接線成分の線積分は、その面 内の法線方向の面積分に等しい。

$$\int \boldsymbol{A}\cdot d\boldsymbol{\ell} =\int (\nabla\times\boldsymbol{A})\cdot\boldsymbol{n}dS$$ (33)

これをストークスの定理と言う。
ホームページ: Yamamoto's laboratory
著者: 山本昌志