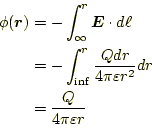1 ガウスの法則と電位
1.1 クーロンの法則
場のベクトル量である電場である。ここで、
から分かっている。これは、ベクトルを使った式ではあるが、諸君が2年生(?) のときに学習したクーロンの法則
 |
(3) |
とほとんど同じであることを理解して欲しい。このときは、スカラーの式なの で、方向を云々と言うような文言がこの式とともに現れたと思う。式 (2)のようにベクトルの式に表すと、余計な文言が不要な ので便利である。ここで、
- 式(1)は定義で、何も物理的なことは語っていない。 したがって、この式が成り立っているか否か、あるいは精度の議論は無 意味である。
- 式(2)は、実験から導かれた式である。この式が、いつ も完全に成り立っているかは不明である。ただ、我々は、この式は非常 に良い精度で成り立っていることを知っているだけである。
実を言うと、本日の学習範囲である真空中の静電場は、この2つの式で全てで ある。過不足なく、この2つの式でおしまいであるが、もう少し便利に計算で きるようにしておく。
これからは、静電場の話をするわけで、力の話はしばらくお目にかからない。 したがって、クーロンの法則は、
と書き換える。物理的な内容は、何も変わっていない。
1.2 発散
話を簡単にするために、座標の原点に1個の電荷- 電場の方向は、
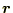 の方向、あるいはその反対である。
の方向、あるいはその反対である。
- 原点からの距離が同じであれば、方向に関わらず、電場の大きさ
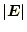 は同じである。
は同じである。
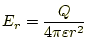 |
(5) |
となる。これを、球の表面で面積分すると
となる。球状の表面の電場を積分したものは、その中に含まれる電荷
ガウスの定理より、式(6)の左辺は、
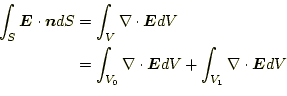 |
のように、変化させることができる。ここで、領域
| (8) |
より、
と書くことができる。今度は、式(6)の球の場 合とは異なり、任意の形状で成り立っている。
このことは、非常にありがたく、わざわざ電荷が原点になくても良いことにな
る。積分する領域の内部にあれば、式(9)が成り立つわ
けである。次に電荷が2個ある場合について考えよう。まずはじめに、
![]() の位置に電荷
の位置に電荷![]() を置いた場合、
を置いた場合、
が成り立つ。次に、この
が成り立つことが分かる。この2つの電荷が同時に存在した場合の電場
| (12) |
となる。これを、各々が独立に存在した領域での表面積分を行うと
となることが分かる。これと同じことを続けると、
 ただし、 ただし、 |
(14) |
ということが分かる。これは便利な式で、ある閉じた領域内にある電荷の総量 は、その閉じた領域の表面での電場を面積分の値と等しいといっている。電荷 の総量を知りたければ、表面での電場を積分すればよい。
この式はなにも、点電荷のみではなく、連続的に電荷が分布している場合も成
り立つ。電荷密度![]() 、これは位置
、これは位置
![]() の関数のスカラー場、を考える。
すると、式(14)の右辺の和の部分は、積分に置着替え
られる。すなわち、
の関数のスカラー場、を考える。
すると、式(14)の右辺の和の部分は、積分に置着替え
られる。すなわち、
のとおりである。これをガウスの法則の積分形と言う。
次に積分の領域を小さくして、ガウスの法則の微分形を考える。まずは、式 (15)の左辺は、ガウスの定理より
である。したがって、式(15)は
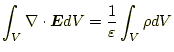 |
(17) |
となる。でもって、積分領域
となる。これがガウスの法則の微分形である。これがマックスウェルの方程式 の最初のものになる。なんのことはない、クーロンの法則を書き直しただけで ある。逆2乗の法則が成り立つと仮定しているから、式 (18)が成り立つのである。
最後に注意を一つ述べておく。式(4)の発散 (divergence)をとり、体積積分してはならない。原点以外の発散はゼロである が、原点は特異点であるため、そこは慎重に取り扱わなくてはならない。
1.3 回転
次に、電場の回転がどうなっているか考える。その前に、電場の線積分を考え る。図1の場合の二つの積分経路AとBの積分を考えると。電 場の線積分の結果は、どちらも同じ値になる。それは、である。どのような経路をとっても、その電場の線積分はスタート点とゴール 点で決まる。
1つ電荷ではなくて、もっとたくさんの電荷がある場合、電場はそのベクトル
和、
![]() となる。したがって、電場
の線積分は、それぞれの線積分
となる。したがって、電場
の線積分は、それぞれの線積分
 |
 |
(20) |
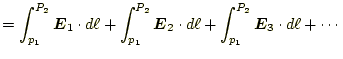 |
(21) |
となる。各々の電荷のつくる電場の線積分は、道筋に依存しないのは先ほど述 べたとおりである。したがって、多くの電荷がある場合、これは任意の静電場 に相当、その線積分は道筋に依存しないと結論できる。
このことから、また別の結論も引き出せる。任意の閉曲線の沿った線積分
 |
(22) |
となる。したがって、静電場の回転は
となる。
以上より、静電場の発散を表す式(18)と回転を示す式 (23)を示すことができた。先週述べたように、発 散と回転が分かったので、これで静電場は決まる。
1.4 スカラーポテンシャルあるいは電圧
静電場では、その回転はゼロであるから、ベクトル解析によれば、となる、スカラー場
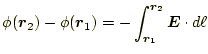 |
(25) |
このスカラー場
![]() のことをポテンシャルと言う。ポテンシャルの
定義式(24)を積分したら得られる。聞きなれた言葉
で言うと、電圧のことである。重力場での高さと同じ役割を果たす。
のことをポテンシャルと言う。ポテンシャルの
定義式(24)を積分したら得られる。聞きなれた言葉
で言うと、電圧のことである。重力場での高さと同じ役割を果たす。
次に、位置の関数としてのポテンシャルを決めたい。一般にポテンシャルの値 に、任意の定数を足し合わせても、その電場の大きさは変わらない。定数は微 分(勾配)すると、ゼロになるからである。ポテンシャルで重要な意味を持つも のは、その差である。どこかに基準を置いて、そこからの差でポテンシャルの 大きさを定義する。ようするに、山の高さは海面を基準にするのと同じである。 あるいは、電気回路において、どこかにアース電位(0V)を決めるのと同じであ る。基準を変えても、物理法則は何も変わらないことに注意が必要である。
通常、無限遠点をポテンシャルの基準とする。すると、
となる。これで、点電荷
もっと一般的に書くと、ポテンシャルは
 |
(27) |
となる。
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成16年9月28日
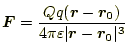

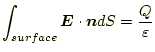
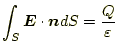

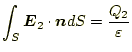
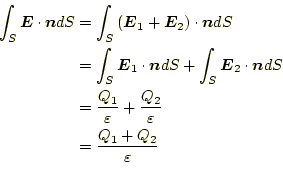

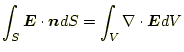


![\includegraphics[keepaspectratio, scale=0.7]{figure/int_E_ds.eps}](img40.png)