Subsections
5 練習問題
- [問1]
- 次に示す数列(フィボナッチ数列)の
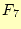 の値は,いくつか?.値のみなら
ず,計算過程も示せ.
の値は,いくつか?.値のみなら
ず,計算過程も示せ.
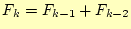
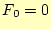
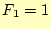
- [問2]
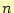 の階乗3を再帰呼び出しで計算するた
めの関数
の階乗3を再帰呼び出しで計算するた
めの関数 を以下に示すが,
=0pt =0.4pt
を以下に示すが,
=0pt =0.4pt
 の内容を選択肢から選べ.
の内容を選択肢から選べ.
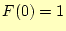
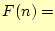 =0pt =0.4pt
=0pt =0.4pt

選択肢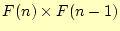

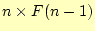
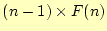
- [問3]
- 問1のフィボナッチ数列を計算するための,再帰呼び出しを使った関数を作 成せよ.
- [問4]
- 問2の
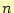 の階乗を計算するための,再帰呼び出しを使った関数を作成せよ.
の階乗を計算するための,再帰呼び出しを使った関数を作成せよ.
- [問5]
- これは応用なので,分からない者は解答する必要はないが,おもしろ
い問題なので興味のある者は調べよ.
- フィボナッチ数列は,どのような場面で登場するか?
- フィボナッチ数列の
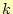 が非常に大きい場合の計算方法を調べよ.
(ヒント : 固有値と固有ベクトルを使う)
が非常に大きい場合の計算方法を調べよ.
(ヒント : 固有値と固有ベクトルを使う)
5.1 レポート提出要領
提出方法は,次の通りとする.
期限 1月16日(月) AM 10:40 用紙 A4 提出場所 山本研究室の入口のポスト 表紙 表紙を1枚つけて,以下の項目を分かりやすく記述すること. 授業科目名「情報工学」 課題名「課題 再帰呼び出し」 2E 学籍番号 氏名 提出日 内容 2ページ以降に問いに対する答えを分かりやすく記述すること.
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
2006-03-23