[Previous: 2 CASL IIの命令語] [Up: CASL IIのまとめ(学年末試験にむけて)] [Next: 4 勉強方法]
Subsections

3 CASL IIのプログラム例

3.1 [例題1]加算

FORTRANやC言語等の高級言語では，メモリーの中のデータ同士を加算して直接メモリーに 格納することができる．FORTRANで次のように加算したとおりである．
      C=A+C
これに対して，アセンブラ言語ではレジスターを通して加算の処理が必要である．先ほど と同じことをするためには，
      LD    GR1,A        ;アドレスAの内容を汎用レジスターGR1にコピー
      ADDA  GR1,B        ;GR1 <-  GR1+ B
      ST    GR1,C        ;GR1の内容をアドレスCにコピー
と書かなくてはならない．加算に限らず，あらゆる演算や処理にレジスターが関わってくる．

コンピューターというものは，メモリーにあるデータをレジスターにコピーして，CPUで 処理して，メモリーにコピーすることを繰り返しているにすぎない．高級言語を用いたプ ログラムでは，それが見えないように隠しているのである．そうすることによりプログラ マーの負担を減らしており，その分コンパイラーが頑張っている．アセンブラー言語の場 合，CPUの動作そのものを記述する必要があるため，メモリーの処理とかレジスターの動 作をその都度書く必要があり，プログラマーは大変である．大変な分，高級言語よりも高 速でメモリーが少なくて動作するプログラムを作ることが可能となる．

3.2 [例題2]加算と条件分岐

条件分岐とは，ある条件に依存して実行される文が変わるようなプログラム構造を言う． 高級言語の場合，条件分岐は実に簡単に実装できる．例えば，変数aとbの大きい方 から小さい方を減算する場合，
	
      if(a<b){
        c=b-a;
      }else{
        c=a-b;
      }
と書けばよい．ここで，if文の括弧の中の演算を制御式と言う．高級言語は，人間 が使っている言葉とほとんど同じで，プログラムが簡単に書ける．

しかし，アセンブラーでは，こんなに簡単ではない．そもそも，if文がないため， それに変わるテクニックを使わなくてはならない．機械語命令を組み合わせて，高級言語 のif文と同じことをするのである．かなりプログラムは面倒であるが，その分コン ピューターのハードウェアー(特にCPU)は簡単になり，高速の動作が可能になる．

アセンブラー言語でifの様な制御文を実現するためには，次のようにする．

  1. 制御式の結果をフラグレジスターに設定する．通常CPAやCPL命令が使 われるが，フラグレジスターが設定できるもので有れば何でも良い．
  2. フラグレジスターの値により，分岐する命令(JPL, JMI, JNE, JZE, JOV, JUMP)を使い，実行する文を選択する．
  3. 実行先は，ラベルで指定する．

教科書の[例題2]では，次のようにしている．

      ADDA  GR1,B        ;GR1=GR1+B  結果の状態がフラグレジスターにセット
      JOV   L1           ;OF(オーバーフローフラグ)が1ならラベル1へ
      JUMP  L2           ;無条件でラベルL2へ

3.3 [例題3]マスク処理と条件分岐

データの特定のビットパターンを選び出すことをマスキングという．このビットパターン を選び出すために，演算を行うわけであるが，その演算のためのデータをマスクと言う． 例えば，教科書のList5-3の場合，2行目のAND GR0,MASKがマスキング(マスク処理) であって，ラベルAのデータがマスクである．このマスクを用いたマスキングにより， GR0特定のビットパターンを選び出している．

教科書の例では偶数か奇数か判断するために，最下位ビットをマスクを用いて検査してい る．ここで用いるマスクパターンは，最下位ビットを調べれば良いので， 0000000000000001となっている． $ (1452)_{10}$ のばあい，それは $ (0000010110101100)_2$ なので

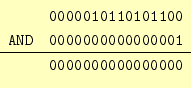\begin{displaymath}\begin{array}{ll} & \texttt{0000010110101100} \\ \texttt{AND}... ...000000000001} \\ \hline & \texttt{0000000000000000} \end{array}\end{displaymath}    

としている．この例から分かるように，論理積(AND)の結果は，ラベルAの最下 位ビットに依存していることが分かる．最下位ビットの1の有無は，フラグレジスタの ZFを見れば分かる．演算の結果，全てのビットがゼロになれば，ZF=1となる．

データの調べたいビットは，マスクにより指定している．このように，調べたいビットを しているデータマスクという．要するに，お面(マスク)で顔の一部を隠すように，興味の ないビットを隠しているのである．

先の例でも分かるが，ANDを使ったマスク処理の場合，マスクは興味の対象のビット を1，どうでも良いビットを0にする．そうすると，興味のないビットは全てゼロとなり， 重要なビットは変更されない．先の場合，ある特定の1ビットの状態が分かれば良かった ので，マスク処理後，直ぐにフラグレジスタZFを見た．もう少し複雑な場合は，こ れではだめである．特定のビットパターンを調べたい場合について考える．例えば，

$\displaystyle \texttt{$\ast\ast\ast\ast$1010$\ast\ast\ast\ast$1100}$    

のような場合である．ここで，$ \ast$ は0でも1でもよく，興味の対象外のビットである．

このようなビットパターンを調べる場合，2つの手順が必要であろう．

  1. まず興味の対象のビットを取り出す必要がある．興味の対象外のビットは， 0または1に設定する．
  2. 興味の対象のビットがある特定のビットパターンになっているか，否か調べる．
これを，ANDとORを使って調べる．

まずは，ANDを使う方法である．調べたいデータはGR0に格納されているとする．

	                 ;これ以前は省略
	   AND  GR0,A    ;マスク
	   CPL  GR0,B    ;ビットパターンの比較
	                 ;このあたりも省略
	A  DC   #0F0F    ;マスク
	B  DC   #0A0C    ;ビットパターンの定義
同じ様なことが，ブール代数の双対の原理2により，ORを使ってもできる．そのほかにも，いろい ろな方法が考えられる．

3.4 [例題4]論理演算とアドレス修飾

図 1: 教科書のList5-4のプログラムを実行する場合のメモリ構造．図中の?は 値はあるが，不明を示している．
r[3pt]6cm
\includegraphics[keepaspectratio, scale=0.8]{figure/memory5-4.eps}
プログラムの命令領域とデータ領域は，図1のようになるだろう．プ ログラムの書き方によっては，こうならないこともあるが，通常はこのようになる．

この場合，プログラムのデータ領域にアクセスする事を考える．ラベルAやBは 簡単で，ラベル名を示せば良い．ラベル名はアドレスを示すからである．問題は，結果を 格納する領域である．このアドレスは，3つ続いて確保されているが，先頭だけANS とラベル名がある．残りの2つの表し方である．これらのアドレスは，ANS+1と ANS+2である．ANSのアドレスにオフセットの値を加算するのである．

プログラムで使うメモリーのアドレスは，ANS+オフセットで，オフセットは， 0,1,2とすれば良い．論理和の結果をANS+0，論理積の結果をANS+1，論理 和の結果をANS+2に格納する．プログラムでは，オフセットの0,1,2をGR2 に入れておき，

	ST     GR1,ANS,GR2
と書く．演算の結果(GR1)の値が，ANSにオフセット値(GR2)を加えたアド レスに格納される．

ここで，使っているGR2のように，1つずつ値が増加するものをカウンターと呼ぶこ とがある．これを使うためには，

とする．このテクニックは，重要である．内容をよく理解する必要がある．

3.5 [例題5]シフト演算

積(かけざん)の演算を行うとき，シフト命令を使えば効率の良いプログラムができる．シ フト命令を使った積の演算は，小学生のときに学習をした筆算の掛け算と同じである．た とえば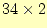， $ 34\times24$ を計算する場合，筆算は $ 34\times(2\times10^{1}+4\times10^{0})$ と分解したはずである．そうして，次の手順 でこの除算を行ったはずである．
  1. $ 34\times2$ を計算し，1桁ずらす(10倍する)．
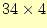  2. $ 34\times4$ を計算する．
  3. 先の計算結果を合計する．この合計816が 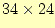$ 34\times24$ の計算結果である．

同じことを2進数で行う．これがコンピューターによる乗算である．先ほどと 同じ計算( $ 32\times24$ )を行う．これを2進数で表現すると，

$\displaystyle (100010)_2\times(11000)_2=(100010)_2\times(1\times2^4+1\times2^3)$    

となる．これを先ほど同様の手順で計算する．
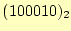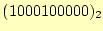  1. 掛け算は1倍なので計算する必要が無く，最初に $ (100010)_2$ を4桁左 にずらす(ビットシフト)．すると， $ (1000100000)_2$ となる．
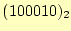  2. 次に $ (100010)_2$ を3桁左にずらす．すると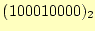， $ (100010000)_2$ となる．
  3. 先の計算結果を合計すると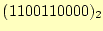， $ (1100110000)_2$ となる．これは，10進 数の816である．
シフトと加算命令でかけ算ができることが分かったはずである．

今回の問題の用に分数の場合でも，

$\displaystyle 0.75$ $\displaystyle =\frac{1}{2}+\frac{1}{4}$    
  $\displaystyle =\left(2^{-1}\right)+\left(2^{-2}\right)$ (1)

と分解する．右に1ビットシフトさせたものと，右に2ビットシフトさせたものを加算すれ ば良い．これを実現するためには，次のようにプログラムを書けばよい．ラベルAの 値を0.75倍した結果をラベルKOTAEに格納する．
	        LAD   GR1,0      ;演算の結果を入れる．初期化
	        LD    GR2,A      ;Aの内容をGR2へ
	        SRA   GR2,1      ;右へ1ビットシフト
	        ADDA  GR1,GR2    ;1ビットシフトした結果を加算
	        LD    GR2,A      ;Aの内容をGR2へ
	        SRA   GR2,2      ;右へ2ビットシフト
	        ADDA  GR1,GR2    ;2ビットシフトした結果を加算
	        ST    GR1,KOTAE  ;演算結果をKOTAEに

教科書のように

$\displaystyle 0.75=1-\left(2^{-2}\right)$ (2)

と分解するのは一般的ではないと思われる．

3.6 [例題6]繰り返し処理

高級言語では繰り返し専用の命令が用意されているが，アセンブラ言語にはない．そのた め，比較命令(CPA,CPL)とジャンプ命令 (JMI,JNZ,JZE,JUMP,JPL,JOV)を上手に使って，繰り返し処理を行うことになる． 教科書では次のようにしている．
	LOOP    LAD   GR2,1,GR2  ;繰り返し処理の始まり
	     省略(いろいろな処理)
	SKIP    CPA   GR1,GR2    ;繰り返し処理終了のためのフラグの設定
	        JPL   LOOP       ;GR1-GR2>0の場合，LOOPへ

3.7 [例題7]繰り返し処理とサブルーチン

何回も使う処理や複雑な処理はサブルーチンという別のプログラムにするのが，定石であ る．そうすることにより，プログラムは簡潔に書け，内容が分かりやすくなる．

CASL IIの場合，サブルーチンと言う別プログラムは，CALL命令を使って呼び出す． サブルーチンでの処理が終わると，RET命令により，呼び出し元へ戻る．教科書の例 では，次のようにしている．

	        CALL  SAIDAI      ;サブルーチンSAIDIの呼び出し
	          省略    
	SAIDAI  LAD   GR1,-1,GR1  ;サブルーチンでの処理の始まり
	          省略
	        RET               ;サブルーチンでの処理の終わり(呼び出し元へ)

サブルーチンは別プログラムではあるが，メモリーやレジスターなどは共有されることに 注意が必要である．

3.8 [例題8]アドレスの受け渡し

利用しやすいサブルーチンを作るためには，その独立性を高めなくてはなら ない．独立性を高めるためには，データの共有を減らすことである．CASL IIの場合，汎用レジス ターを使ってデータの受け渡しを行う．また，汎用レジスターはデータの処理にも使われ る．サブルーチンでは，できるだけ汎用レジスターの値を変更しないようにする．これを 実現するためには， とすれば良い．こうすれば，呼び出し元とサブルーチン間のデータの受け渡しは汎用レジ スターを通しておこなわれ，その値の変化は必要最小限に抑えられる．他に影響が無いの で，サブルーチンの独立性は高くなる．

3.9 [例題9]ラベルを2重に付ける方法

教科書の例題6(p.97)〜8(p.101)は，いずれも与えられたデータの最大値を求めるプログ ラムであった．これらの場合，最大値を求めたいデータの数列とその数が与えられていた． データ数を元に，数列を読みしと比較を繰り返すことにより最大値を探索した．ここでは， データ数が与えられていない場合，ラベルを2重につけてデータの終わりを示す．

教科書のプログラムの内容は，

である．このプログラム例で学習することは，最終データがあるアドレスにラベル名をつ けることである．それは，プログラム中で示しているように
	DATA  DC   1,5,6,8,9    
	LAST  DS   0      ;数列の最終アドレス+1
とするのである．こうすると数列の先頭のアドレスはDATAで，最終アドレスは LAST-1で示すことができる．

3.10 [例題10]数値データを文字データに変換

3.10.1 文字コードに変換

マクロ命令のOUTを用いて，出力装置に数値を打ち出す場合，数値を文字データに変 換しなくてはならない．なぜならば，OUTが出力できるのは文字に限られるからであ る．たとえば，整数の $ (2345)_{10}$ を出力装置で打ち出す場合，#0032, #0034, #0034, #0035 と言うデータが必要である．これは，文字コードの規格で，数字(0〜9) が文字コードの#0030〜#0039に割り当てられているからである．

そのような理由で，整数(0〜9)の値に#0030を加えれば文字コードに変換できる． いろいろな方法が有るが，教科書では次のようにしている．

      OR    GR3,MOJI     ;#0030を加算　　MOJI=#0030

3.10.2 わり算

教科書のプログラムでは，割り算の演算も必要で，商と余りが計算できなくてはならない． それは何回も使うのでサブルーチンにしている．このサブルーチンのわり算の方法は簡単で， としている．これは，除数も被除数も正と仮定しているためこのようなことができる．負 の数を考えるともう少し複雑なことを考えなくてはならない．

3.11 [例題11]文字データを数値データに変換

マクロ命令のINを使って，キーボードから数値を読み込みたい．問題は，この命令 で読み込まれるのは文字であるということである．整数を入力しても，それは文字として 処理され，指定されたメモリーに人文字ずつ格納される．すなわち，-102とキーボー ドから入力された場合，メモリーには文字コード表に従い#002D, #0031, #0030, #0032と格納される．このキーボードから入力された整数(-102)を演算に利用する ためには，文字コード化された整数を数値に変換する必要がある．

この文字コードと整数の対応を見ると，文字コードの最後の4ビットが整数に対応してい ることが分かる．この4ビットを取り出すのは簡単で，マスク処理を行えば良い．教科書 では，汎用レジスターGR3に文字を入れて，それをマスク処理して，整数に変換して いる．つぎのようにである．

      AND   GR3,=#000F   ;マスク処理　最後の4ビットを取り出して，整数化

最後に，先頭の負号の確認を行う必要がある．先頭の文字が負号な らば，ラベルMINUSへ処理が移すために，教科書では次のようにしている．

      CPA   GR3,='-'     ;先頭の桁の処理  先頭をGR3に入れて'-'と比較
      JZE   MINUS        ;マイナスの時は分岐　　GR3が'-'ならばMINUSへ

そして，マイナスの場合は絶対値の処理が必要で，-1倍すればよい．それは2の補数にす ればよく，ビット反転と1加算すると実現できる．1との排他的論理和(XOR)を計算す ることにより，ビット反転はできる．教科書のプログラムでは，-1倍は次のようにしてい る．

 MINUS  XOR   GR0,=#FFFF  ;ビット反転
        ADDA  GR0,=1      ;+1加算

3.11.1 かけ算

教科書のプログラムでは，かけ算の演算も必要である． それは何回も使うのでサブルーチンにしている．このサブルーチンのかけ算の方法は簡単で， としている．

[Previous: 2 CASL IIの命令語] [Up: CASL IIのまとめ(学年末試験にむけて)] [Next: 4 勉強方法]
[Top:ページの先頭に戻る]

ホームページ: Yamamoto's laboratory
著者: 山本昌志
Yamamoto Masashi
2006-02-25

no counter