4 配列と文字列(教科書の4章)

4.1 配列とは

3節で示した変数⁵の場合、 一度に確保できるメモリーの領域は1個なので、大量のデータを扱うのは不向きである。 変数だけを使って、100万個のデータを扱うことは不可能である。100万個の変数名 を用意するのはナンセンス。そこで、順序づけられた同じ型のデータが複数ある場合、配 列というデータ構造が考えられた。

これは、同じ型のデータを任意の個数宣言し、配列名と自然数 ⁶でアクセスすることができるようにしたもの である。配列を使うためには、

	int i[10], j[100][100];

のように宣言をする。こうすると、

• 配列名iの整数型のデータ領域が10個用意される。用意されるデータ領域 は、i[0]〜i[9]である。
• 配列名jの整数型のデータ領域が10000個用意される。用意されるデータ領域 は、j[0][0]〜j[99][99]である。。

となる。図2のように、メモリー領域が確保される。このデータ構 造では、配列名と添え字(インデックス)、たとえばi[3]やj[25][49]を指定す ることで、その領域から値を入出力できる。

	i[3]=5;         /* 配列 i[3] に 5 を代入　*/
	c=j[25][49];    /* 配列 j[25][49] の値を変数 c へ代入 */

図 2: 配列のイメージ。データを入れる箱がいっぱいある。ただし箱の大きさは全 て同じ。

添え字が1つのものを一次元配列と言い、それ以上のものを多次元配列と言う。C言語では 多次元配列を使う場合、

	
	int hoge_1[100], hoge_2[100][100], hoge_3[100][100][100];
	double huga[10], huge[10][10], hugo[10][10][10];

のように宣言を行う。これらも、配列名と複数の添え字で、そこにあるデータにアクセス する事ができる。3次元以上ももちろん可能である。

4.2 数列、ベクトル、行列を配列で表現

一次元の配列は数学の数列とベクトルと、二次元の配列は行列とよく似ている。実際、数値計算で 数列やベクトル、行列に関わる数値演算を行うときには、配列が使われる。これ らの数学の表現も、やはり順序づけられた数の集まりにすぎないので、配列と同じである。 一方、スカラー量の場合には、通常の変数として扱えばよい。

数列やベクトル、行列の成分を表す場合、下添え字がつく。その添え字と同じように、配 列の添え字を使う。実に簡単である。ただし、数学の場合、添え字が 1 から始まること が多いが、C言語の場合、それは 0 から始まるので注意が必要である。配列の宣言の時、 添え字部分に書かれるのは要素数であるので、ベクトルや行列の要素数に 1 を加えた数 で領域を確保しなくてはならない。必要数より大きめに確保するのが普通である。

1. 数列やベクトルを配列で表現

2. 行列を配列で表現

表 1: 数列やベクトルを配列で表現

数学	C言語
$a_1$	a[1]
$a_2$	a[2]
$a_3$	a[3]
$\vdots$	$\vdots$
$a_i$	a[i]
$a_{i+1}$	a[i+1]
$\vdots$	$\vdots$
$a_{2i+1}$	a[2*i+1]
$\vdots$	$\vdots$

表 2: 行列を配列で表現

数学	C言語
$a_{1 1}$	a[1][1]
$a_{1 2}$	a[1][2]
$a_{1 3}$	a[1][3]
$\vdots$	$\vdots$
$a_{3 3}$	a[3][3]
$a_{3 4}$	a[3][4]
$\vdots$	$\vdots$
$a_{i j}$	a[i][j]
$\vdots$	$\vdots$
$a_{i+1 j+1}$	a[i+1][j+1]
$\vdots$	$\vdots$
$a_{2i+1 3j+2}$	a[2*i+1][3*j+2]
$\vdots$	$\vdots$

4.2.1 乗算

配列を使って行列とベクトルのかけ算を行うソースをプログラム 3にしめす。この例は要素数が少ない場合であるが、多くな ると、後で学習する繰り返し処理が必要となる。言うまでもないと思うが、行列とベクト ルのかけ算

$$\begin{aligned}\begin{bmatrix}a_{11} & a_{12} & a_{13} & \ldots... ... \\ c_{2} \\ c_{3} \\ \vdots \\ c_{n} \end{bmatrix} \end{aligned}$$

の演算は、

$$c_i=\sum_{\ell=1}^n a_{i\ell}b_{\ell}$$ (2)

である。

$n=2$の場合の計算を行うプログラム 3の各行の内容は以下の通りである。

3行

実数型の配列を宣言。

5-11行

配列(行列とベクトル)の要素に値を代入。

13-14行

行列とベクトルの乗算。

[練習1]

プログラム3を参考にして、 $\boldsymbol{Mx}$を計算するプログラムを作成せよ。

$$\begin{aligned}& \boldsymbol{M}= \begin{bmatrix}1 & 2 & 3 \ 4 ... ...symbol{x}= \begin{bmatrix}1 \ 2 \ 3 \end{bmatrix} \end{aligned}$$

4.2.2 フィボナッチ数列

次のサンプルプログラムは、フィボナッチ(Fibonatti)数列の問題である。

フィボナッチのウサギ

成熟した1つがいのウサギは、1ヶ月後に1つがいのウサギを生むとする。そして、生まれ たウサギは1ヶ月かけて成熟して次の月から毎月1つがいのウサギを生む。全てのウサギ はこの規則に従うとし、死ぬことは無いとする。1つがいのウサギは、1年後には何つが いになるか。2、3年後はどうなっているだろうか?。計算してみると分かるが、恐ろしい ことになっている。

この数列は単純で、

$$\left\{ \begin{aligned}&F_0=1 \ &F_1=2 \ &F_{k}=F_{k-1}+F_{k-2} \end{aligned} \right.$$

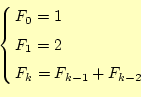となっている。この単純な数列が、自然界のいろいろな場所でお目にかかれるらしい。か なり不思議なことのようなので、興味のあるものは調べてみると良い。

フィボナッチ数列$F_k$を計算するソースをプログラム4にしめす。 各行の内容は以下の通りである。

9-11行

for文(教科書p.142)は繰り返しに使われる。ここでは、変数 tuki の値を2〜36まで、一つずつ増加させている。中括弧{ } 内の文を1 回実行させるたびに、変数tukiの値を増やしている。

[練習1]

消費者金融の利子を見ると恐ろしいものがある。CMなどをみ ると年間20%前後である。100万円借りた場合、次の単利と複 利の場合の10年後の利息を計算せよ。

• 単利の場合、元金の100万円のみに利子が付く。
• 複利の場合、元金と利息にも利子が付く。

[練習2]

時間が余った者のみ、チャレンジせよ。この問題は参考文献  [1]から引用した。

Bernadelliはある種類のカブトムシについて考察した。その カブトムシは、3年間で成長し、3年目につぎの世代を生んで 死亡する。3年間のうち第一年目で確率 1/2 で生き残り、さ らに第2年目で 1/3 が生き残り、第3年目でそれぞれの雌が6 匹の雌を生む。これに対応する行列は、

$$\begin{bmatrix}b_{k 1} \ b_{k 2} \ b_{k 3} \end{bmatrix}= \b... ...nd{bmatrix} \begin{bmatrix}b_{k-1 1} \ b_{k-1 2} \ b_{k-1 3} \end{bmatrix}$$

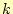とかける。ここで、$b_{k 1}$は$k$年のときの1年目のカブ トムシの数である。

1年目、2年目、3年目の虫がそれぞれ3000匹いた としたときその年以後6年間の虫の分布を求めよ。

4.3 文字列

これは、数値計算ではあまり使わないので、興味のあるものは教科書を読んでおくように。
ホームページ: Yamamoto's laboratory
著者: 山本昌志