6 練習問題

6.1 ガウス・ジョルダン法

1. 次の連立方程式をピボット選択無しのガウス・ジョルダン法で計算するプログラ ムを作成しなさい。プログラムは、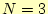$N=3$ のみならず、$N=100$ 程度まで容易に計算 できるように汎用的にすること。

   $$\left\{ \begin{aligned}2x-4y+6z&=5 -x+7y-8z&=-3 x+y-2z&=2 \end{aligned} \right.$$

   
   

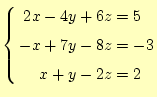
2. プログラムが完成したら、逆行列を計算するルーチンも追加しなさい。そして、 逆行列と元の行列をかけ合わせたら単位行列になることを確認しなさい。
3. 逆行列が完成したら、ピボット選択のルーチンを追加しなさい。
4. ピボット選択のルーチンが完成したならば、次の連立方程式を計算しなさい。

   $$\begin{aligned}a_{ij}&=\cos\left[\frac{\pi (i-1)(j-1)}{N}\right... ...\cdots,N b_i&=\frac{i-1}{N} \qquad i=1,2,\cdots,N \end{aligned}$$

   
   
   これは、三角波のフーリエ変換(離散フーリエ変換)になっている。とりあえず、 N=100程度で計算してみて、最後に

   $$\begin{aligned}f(x)=\sum_{j=1}^{N}x_i\cos\left[(j-1)x\right] \end{aligned}$$

   
   
   をプロットして三角波になっていうることを確認せよ。

ホームページ: Yamamoto's laboratory
著者: 山本昌志