Subsections
5 LU分解
5.1 LU分解による解の計算方法
係数行列| (14) |
下三角行列と上三角行列の要素を書き出すと
となる。
このようにLU分解できると、連立1次方程式は
| (16) |
と書ける。これをさらに書き換えると、
となる。これらの連立方程式の解
 |
である。この
![[*]](crossref.png) )の
)の
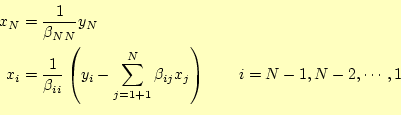 |
これらの前進代入と後退代入は、コンピューターにとって非常に簡単に計算できる。これ
は、係数行列![]() をLU分解できれば、連立方程式は簡単に解けると言っている。次節でLU
分解の方法を詳しく説明する。
をLU分解できれば、連立方程式は簡単に解けると言っている。次節でLU
分解の方法を詳しく説明する。
いったんLU分解が出来てしまえば、式(1)の右辺
![]() が変わっ
ても、そのLU分解の形を変える必要がない。右辺が変わっても、LU分解は1回で済む。こ
れが、ガウスの消去法と後退代入を組み合わせた方法やガウス・ジョルダン法に比べて、
際立って優れている点である。
が変わっ
ても、そのLU分解の形を変える必要がない。右辺が変わっても、LU分解は1回で済む。こ
れが、ガウスの消去法と後退代入を組み合わせた方法やガウス・ジョルダン法に比べて、
際立って優れている点である。
5.2 LU分解(クラウトのアルゴリズム)
LU分解するということは、式(15)の| (21) |
とする。
それでは、クラウトのアルゴリズムによるLU分解の手順を示すことにする。
-
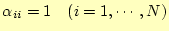 とします。この操作により、解
くべき行列方程式(15)は
とします。この操作により、解
くべき行列方程式(15)は
と変形できる。 - この式を見ると、
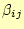 と
と
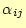 が次に示す順序で簡単に求められ
ることが分かる。まずは式を見て分かるように、
が次に示す順序で簡単に求められ
ることが分かる。まずは式を見て分かるように、
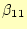 が直ちに計算できる。
次に
が直ちに計算できる。
次に
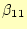 を利用して、
を利用して、
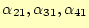 を求める
ことができる。これで、
を求める
ことができる。これで、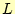 と
と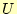 の第1列目が求められた。次に第2列目である。こ
れも
の第1列目が求められた。次に第2列目である。こ
れも
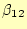 は直ちに計算できる。そうして、これまで分かっている
は直ちに計算できる。そうして、これまで分かっている
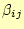 と
と
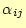 を使うと、
を使うと、
 を求めることができる。これで第2列目は終わりで、同じことを繰り返すと、全て
の
を求めることができる。これで第2列目は終わりで、同じことを繰り返すと、全て
の
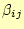 と
と
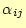 が計算できる。これをアルゴリズムにすると次の
ようになる。
が計算できる。これをアルゴリズムにすると次の
ようになる。
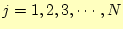 という順序で計算する。
という順序で計算する。
 と
と
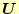 の
の 列目を計算することになる。具体的には、以下のようにして、
列目を計算することになる。具体的には、以下のようにして、 列目の
列目の
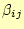 と
と
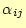 を求める。
を求める。
- まず、
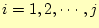 について、次式に従い
について、次式に従い
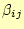 を
計算する。
を
計算する。
- 次に、
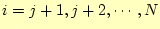 について、
について、
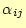 を計算する。
を計算する。
- これで、
 と
と
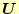 の
の 列目が完成したので、同じ操作を
列目が完成したので、同じ操作を
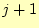 列目に行う。同じことを繰り返して、LU分解の行列を
完成させる。
列目に行う。同じことを繰り返して、LU分解の行列を
完成させる。
- まず、
この方法により、LU分解ができる。次に示すピボット選択をしなければ、アルゴリズムは 非常に単純である。
5.3 ピボット選択
ここでも、ピボット選択の問題が出てくる。式(24)の
ではどうするかですが、これも途中(![]() 列)まで分解した行列は崩したくない。そのため
には、行列
列)まで分解した行列は崩したくない。そのため
には、行列
![]() の行を交換し、それに対応した行列
の行を交換し、それに対応した行列
![]() の行を交換すれば問題
がもっとも少なくなる。当然、行列
の行を交換すれば問題
がもっとも少なくなる。当然、行列
![]() は行も列も変化しない。最終的には行を交換
した行列
は行も列も変化しない。最終的には行を交換
した行列
![]() のLU分解が出来る。連立1次方程式を解くときには、同様に
のLU分解が出来る。連立1次方程式を解くときには、同様に
![]() の行も交換しておく。ただし、行の交換であるため、解
の行も交換しておく。ただし、行の交換であるため、解
![]() の要素の順序は
入れ替わらない。
の要素の順序は
入れ替わらない。
つぎに、どのようにして交換する行を決めるかである。一般的には、
![]() が大き
くなるように選択すれば良い結果が得られる。クラウト法のピボット選択は、次のように
進める。
が大き
くなるように選択すれば良い結果が得られる。クラウト法のピボット選択は、次のように
進める。![]() 列目のピボットを選択する場合についてである。
列目のピボットを選択する場合についてである。
- まずは、
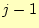 列目までの行列
列目までの行列
 の各行の要素の最大値を1に規
格化する。同時に、対応する行列
の各行の要素の最大値を1に規
格化する。同時に、対応する行列
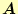 の行も同じ係数を掛ける。
の行も同じ係数を掛ける。
- そうして、
を計算する。これは、式(23)と同じ、 式(24)と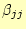 で割ること以外は同じであ
ることに注意が必要である。
で割ること以外は同じであ
ることに注意が必要である。
- 最大の
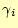 となるものをピボットとして選択する。
となるものをピボットとして選択する。
- 最大のピボットとなる行が分かったので、後は元(規格化前)の
 と
と
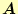 を用いて、式(24)と
を用いて、式(24)と
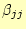 を計算する。
を計算する。
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
2005-11-18