2 簡単な例

2.1 連立一次方程式

ガウス・ザイデル法で連立一次方程式

$$\begin{bmatrix}3 & 2 & 1 \ 1 & 4 & 1 \ 2 & 2 & 5 \end{bmatrix} ... ...ix}x_1 \ x_2 \ x_3 \end{bmatrix} = \begin{bmatrix}7 \ 12 \ 19 \end{bmatrix}$$ (1)

を計算する方法を示す．この方程式の解析解は，

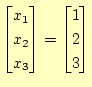$$\begin{bmatrix}x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix}1 \\ 2 \\ 3 \end{bmatrix}$$ (2)

であるが，計算機でこれを求めることにする．前回の講義で示したガウス・ザイデル法の漸化式 は

$$x_i^{(k+1)}=a_{ii}^{-1}\left\{b_i-\left[ a_{i1}x_1^{(k)}+a_{i2}x_... ...x_{i-1}^{(k)}+a_{ii+1}x_{i+1}^{(k+1)}\cdots +a_{in}x_{n}^{(k+1)}\right]\right\}$$ (3)

である．これは，反復の$k$ 番目の近似解から，より精度の良い$k+1$ 番目の解を求める方法を表し ている．

これを，式(1)に当てはめると

$$x_1^{(k+1)}=\frac{1}{3}\left[7-2x_2^{(k)}-x_3^{(k)}\right]$$ (4)

$$x_2^{(k+1)}=\frac{1}{4}\left[12-x_1^{(k+1)}-x_3^{(k)}\right]$$ (5)

$$x_3^{(k+1)}=\frac{1}{5}\left[19-2x_1^{(k+1)}-2x_2^{(k+1)}\right]$$ (6)

である．当然，これは $x_1^{(k+1)}\rightarrow x_2^{(k+1)}\rightarrow x_3^{(k+1)}\rightarrow$ の順序で計算を進める．もう少しくだけた見方をする と，この式は連立方程式式(1)

$$3x_1+2x_2+x_3=7$$ (7)

$$x_1+4x_2+x_3=12$$ (8)

$$2x_1+2x_2+5x_3=19$$ (9)

から，各行の $x_1, x_2, x_3$ を解いている式と

$$x_1=\frac{1}{3}\left(7-2x_2-x_3\right)$$ (10)

$$x_2=\frac{1}{4}\left(12-x_1-x_3\right)$$ (11)

$$x_3=\frac{1}{5}\left(19-2x_1-2x_2\right)$$ (12)

と同一である．式(7)から式(10)を，式(8) から式(11)を，式(9)から式(12)を導いてい るのである．ガウス・ザイデル法の漸化式(4),(5),(6)は， 連立方程式を変形した式(10),(11),(12)とそっ くりである．最初にガウス・ザイデル法を考えた人(ザイデル???)は，連立方程 式を式(10)〜(12)のように変形して，繰り返し計算を行えば 真の解に近づくと考えたのだろう．ちょっと数値計算になれた者であればすぐに気がつくア ルゴリズムである．

2.2 プログラム例

漸化式が求められたので，実際のプログラムを書いてみよう．プログラムの例をリスト 1に示しておくので，よく理解せよ．

   1 #include <stdio.h>
   2 #include <math.h>
   3 #define N (3)
   4 #define EPS (1e-15)
   5 
   6 int main(){
   7   double a[N+1][N+1], x[N+1], b[N+1];
   8   double error, absx, temp, new;
   9   int i,j;
  10 
  11   a[1][1]=3.0;  a[1][2]=2.0;  a[1][3]=1.0;
  12   a[2][1]=1.0;  a[2][2]=4.0;  a[2][3]=1.0;
  13   a[3][1]=2.0;  a[3][2]=2.0;  a[3][3]=5.0;
  14 
  15   b[1]=10.0;
  16   b[2]=12.0;
  17   b[3]=21.0;
  18 
  19   x[1]=0.0;
  20   x[2]=0.0;
  21   x[3]=0.0;
  22 
  23   do{
  24     error=0.0;
  25     absx=0.0;
  26 
  27     for(i=1;i<=N;i++){
  28       temp=0.0;
  29       for(j=1;j<=N;j++){
  30 	temp+=a[i][j]*x[j];
  31       }
  32       new=1.0/a[i][i]*(b[i]-(temp-a[i][i]*x[i]));
  33       error+=fabs(new-x[i]);
  34       absx+=fabs(new);
  35       x[i]=new;
  36     }
  37   }while(error/absx > EPS);
  38  
  39   for(i=1;i<=N;i++){
  40     printf("x[%d]=%25.20lf\n",i,x[i]);
  41   }
  42 
  43   return 0;
  44 }

ホームページ: Yamamoto's laboratory
著者: 山本昌志