1 常微分方程式
1.1 常微分方程式のイメージ
微分方程式は、物理や工学の分野で問題を解く強力なツールばかりか、生物や経済などで も広く応用されている。自然科学や工学の問題を定量的に考察する場合、微分方程式ほど 強力な道具はない。この微分方程式を使うためには、方程式をる作ことと解くことが必要 である。ここでは、微分方程式を解くこと、特に数値計算により非常に精度の良い近似値 を求める方法を学習する。微分方程式には解析解が無いのが普通であるが、理工学上の諸 問題では精度良く解の近似値を求めたい状況にしばしば遭遇する。このような時、数値計 算の出番となる。数学に無い面白さがありますので、楽しんでください。すでに学習したように、独立変数が二つ以上の多変数の関数の微分(偏微分)を含む微分方 程式を偏微分方程式(partial differential equation)という。それに対して、一変数の 関数の微分を含む方程式を常微分方程式(ordinary differential equation)という。ここ では、常微分方程式、特に1 階の場合の解の近似値を求める方法を学習する。学習する方 程式の形は
である。1階だといってバカにはできない。後で述べることになるが、これが数値計算 できると、どんな高階の常微分方程式も同じ方法で計算ができるのである。数学だと1 解 が解ければ高階の微分方程式が解けるわけではないが、数値計算では可能なのである。
ここでの主題は、この微分方程式を満たす![]() を求めることになる。計算を進める前に、
この方程式が何を表すか考えることにする。式(1) の左辺は、解
を求めることになる。計算を進める前に、
この方程式が何を表すか考えることにする。式(1) の左辺は、解![]() の導関数となっている。即ち、解の曲線の接線を表す。導関数の値が座標
の導関数となっている。即ち、解の曲線の接線を表す。導関数の値が座標![]() の関数になっ
ているので、座標が決まれば、その場の曲線の傾きが決きまることになる。
の関数になっ
ているので、座標が決まれば、その場の曲線の傾きが決きまることになる。
それでは、この常微分微分方程式のイメージをつかむことにする。それには、実際 の微分方程式を考えるのが良いであろう。例えば、
のような常微分方程式を考えることにする。いかにも難しげな微分方程式であるが、これ には解析解がある。解析解はとりあえずおいておくことにして、この式の右辺を考える。 先ほど述べたように、これは接線の傾きを表す。座標によって、接線の傾きが決まってい るので、それをを図示する。各座標の傾きを線の傾きで表すと、図 1のようになる。この傾きを方向場と言う。方向場から、大体 の解の様子がわかる。
この部分方程式の解析解は、
| (3) |
である。1階の微分方程式なので、1個の未知数を含む。この未知数の値が異なる5本の曲 線と、先ほどの方向場を重ねて書きすると、図2のようになる。微分方 程式の解である曲線
式(2)の微分方程式から、関数![]() の値を得るにはもう一つ条件が必
要である。通常この条件は、
の値を得るにはもう一つ条件が必
要である。通常この条件は、
![]() のように与えられる。これを初期値といい、初
期値が与えられるものを初期値問題という。一方、2 点以上のxで定めるyの値が決まって
いるような問題を境界値問題という2。ここでは、もっぱら初期値問題
を解くことにする。
のように与えられる。これを初期値といい、初
期値が与えられるものを初期値問題という。一方、2 点以上のxで定めるyの値が決まって
いるような問題を境界値問題という2。ここでは、もっぱら初期値問題
を解くことにする。
1.2 数値計算のイメージ
初期値問題を計算するルーチンの基礎的な考え方はどれも似通っており、次に述べるとお りである。。まず(1)式の微分方程式を、極限の| (4) |
のように近似できる。これを用いて、
この式と初期値
式(5)は、
- 次の
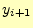 値は、もとの
値は、もとの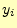 に、そこでの傾き
に、そこでの傾き
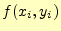 に
に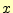 の増分
の増分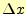 を乗じたものを加えることにより求められる。
を乗じたものを加えることにより求められる。
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成19年6月24日
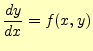
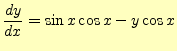
![\includegraphics[keepaspectratio, scale=1.0]{figure/direction_field.eps}](img25.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/solution.eps}](img28.png)
![\includegraphics[keepaspectratio, scale=0.7]{figure/sabun.eps}](img51.png)