2 数値計算法
2.1 オイラー法
常微分方程式を数値計算で解く方法として、もっとも単純ではあるが、最も精度の悪い方 法でる。よっぽどのことが無い限り、この方法で微分方程式を計算してはならない。ただし、 常微分方程式を数値計算することのイメージがつかみやすいので、学習する勝ちはある。もう一度、初期条件を含めて数値計算により解くべき方程式を示す。
 |
初期条件 | (6) |
この微分方程式の解を
となる。この式の右辺第2項は、式(6) から計算で きる。したがって、テイラー展開は、
| (8) |
と表すことができる。
オイラー法での数値計算では、計算の刻み幅![]() は十分に小さいとして、
は十分に小さいとして、
| (9) |
を計算する。式(5)と全く同じである。このとき計算の精度は1次と 言う。3。
オイラー法をまとめると、以下に示すように微分方程式は差分方程式に近似できる。
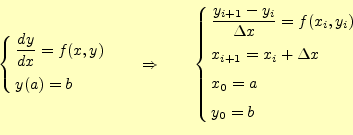 |
これれから、オイラー法での数値計算の漸化式
 |
となる。初期値
実際にプログラムを行うときは、forやwhileを用いて繰り返し計算を行う(芋
づる式の部分)。そして、計算結果の![]() と
と![]() は、配列x[i] やy[i]に格納
する。
は、配列x[i] やy[i]に格納
する。
x[0]=a;
y[0]=b;
while(計算終了条件){
delta_x や delta_y の計算
x[i+1]=x[i]+delta_x;
y[i+1]=y[i]+f(x[i],y[i])*delta_x;
}
この方法の計算のイメージは、図4の通りである。明らかに、出発 点の導関数のみ利用しているために精度が悪い。式も対称でないため、逆から計算すると 元に戻らない。
- [練習1]
- 以下の微分方程式をオイラー法で計算して見よ。最初は刻み
幅を2として、
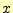 の範囲[0,10]で計算せよ。次に、刻み幅を
その半分にして見よ。
の範囲[0,10]で計算せよ。次に、刻み幅を
その半分にして見よ。
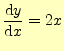
(12)
初期条件は、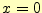 の時、
の時、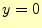 とする。
とする。
2.2 2次のルンゲクッタ法
2次のルンゲ・クッタと呼ばれる方法は、いろいろある。ここでは、代表的なホイン法と 中点法を示す。オイラー法は1次の精度であったが、これらは2次の精度になる。2.2.1 ホイン法
2.2.1.1 漸化式
先に示したように、オイラー法の精度は1次です。それに対して、2次のルンゲ・クッタ法 の精度は2次となる。今まで刻み幅を2次の精度ということは、テイラー展開より
| (13) |
となっていることを意味する。即ち、計算アルゴリズムが、
となっている必要がある。
式(14)から分かるように、![]() の増分
の増分![]() を計算するためには、
1階微分と2階微分の2項を満たす式が必要である。そうすると少なくとも、2点の値が必要と
なる。2点として、計算区間の両端の導関数の値を使うことにする。この導関数は問題とし
て与えられているので、計算は簡単である。そうして、区間の増分を
を計算するためには、
1階微分と2階微分の2項を満たす式が必要である。そうすると少なくとも、2点の値が必要と
なる。2点として、計算区間の両端の導関数の値を使うことにする。この導関数は問題とし
て与えられているので、計算は簡単である。そうして、区間の増分を
![]() のパ
ラメーターとした和で表現する。即ち、
のパ
ラメーターとした和で表現する。即ち、
とあらわすのである。この
![[*]](crossref.png) )と同一にできる。
)と同一にできる。
この式を![]() の回りでテイラー展開すると
の回りでテイラー展開すると
| (16) |
となる。これを、式(14)と比べると、
 |
が得られる。これで、必要な式は求まった。まとめると、式 (6)を数値計算で近似解を求めるには
を使うことになる。何のことはない、出発点と終着点の平均の傾きを使っているのである。 この式のイメージは、図5の示すところである。オイラー法では、区間の 平均の傾きを出発点だけで決めていたが、ホイン法は両端で決めているのである。これに より、計算精度が向上するのである。
2.2.1.2 精度の検証
よく見ると、この式(18)は、本当に2次の精度なのか?、と疑問が湧く。まずは、少なくとも2次の精度があることを確認である。漸化式は、
と変形できる。この結果は、まさに式(7)と同じ形をしており、少なくとも 2次の精度があることが確認できる。
次に3次の精度がないことを示す。テイラー展開の3次の項は、係数は無視すると、
となる4。
一方、ホイン法の3次の精度を表すのは、式(19)の右辺のテ イラー展開の2次の項である。これは、
となる。
明らかに、テイラー展開の3次の項である式(20)とホイ ン法の3次の項の式(21)は異なっている。したがって、ホイ ン法は3次の精度がないことが分かる。少なくとも2次の精度があって、3次の精度がない ことが示されわけで、、ホイン法は2次の精度であることが証明されたことになる。
2.2.2 中点法
2.2.2.1 漸化式
これも、ホイン法と同じ2次の精度である。ホイン法は区間の両端の点の導関数 を使ったが、中点法は出発点と中点で漸化式を作る。先ほど同様、2点を使うので、2次の精度 にすることができる。ホイン法の式(15)に対応するものは、である。これを
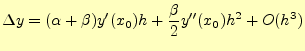 |
(23) |
となる。これを、式(14)と比較すると、
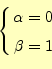 |
となる必要がある。したがって、中点法の漸化式は、
となる。この公式のイメージを、図6に示しておく。
2.2.2.2 精度の検証
式(19)と同じ手順でを用いることにより、中点法が2次の精 度であることが証明できる。漸化式をテーラー展開すると、が導かれる。ホイン法の場合と同様、これは、式(7)の2次の部分まで等 しいので、少なくとも2次の精度があることが分かる。一方、3次の精度がない ことは、以下の通り明らかである。式(21)と比べ て、微小変位
と直ちに導くことができる。これは、式(20)と異なりま すので、3次の精度がないことがはっきりしている。
2.3 4次のルンゲ・クッタ法
今まで示したオイラー法や2次のルンゲ・クッタ法のように、パラメーターを増やして誤 差項の次数を上げていく方法で、最良の方法と言われるのが4次のルンゲ・クッタ法であ る。パラメーターを増やして、5, 6, 7,
ということで、皆さんが常微分方程式を計算する必要が生じたときは、何はともあれ4次
のルンゲ・クッタで計算すべきである。「この問題を解く場合、4次のルンゲクッタだな」
と一言いって、プログラムを書き始めると、出来るなと思われること間違いなしである。
間違っても「2次のルンゲ・クッタ![]() 」と言ってはいけません。「4次の方が
」と言ってはいけません。「4次の方が
![]() 」と言う輩が必ずでてくる。普通の科学に携わる者にとって、4次のルンゲ・クッ
タは常微分方程式の最初で最後の解法である。
」と言う輩が必ずでてくる。普通の科学に携わる者にとって、4次のルンゲ・クッ
タは常微分方程式の最初で最後の解法である。
ただし、4次のルンゲ・クッタ法よりも精度の良い方法があることも知っておく必要があ る。より高精度な方法として、Bulirsch-Store法や予測子・修正法などがある。進んだ勉強を したいときに、学習するのがよいだろう。
4次のルンゲ・クッタの公式は、式(28)に示す通りである。そして、これ のイメージは図7のように表すことができる。
2次の場合と同じ手順で、公式を導き、そして4次の精度であることが証明できるであろう。 しかし、計算は明らかに大変なので、腕力のある人はトライせよ。
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成19年6月24日
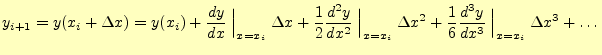
![\includegraphics[keepaspectratio, scale=1.0]{figure/Euler.eps}](img76.png)
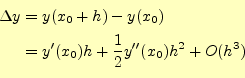
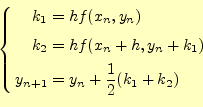
![\includegraphics[keepaspectratio, scale=1.0]{figure/RK2_1.eps}](img101.png)

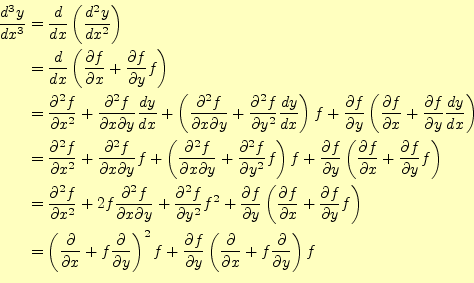
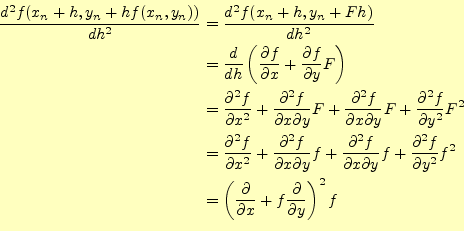
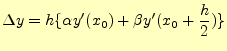
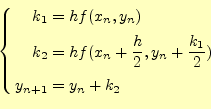
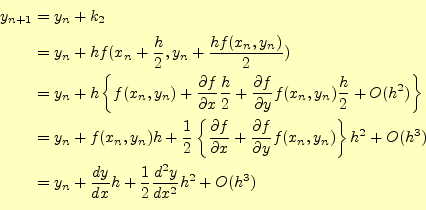
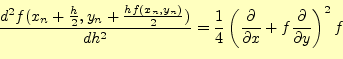
![\includegraphics[keepaspectratio, scale=1.0]{figure/RK2_2.eps}](img126.png)

![\includegraphics[keepaspectratio, scale=1.0]{figure/RK4.eps}](img137.png)