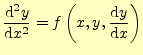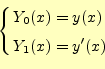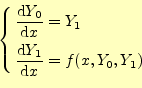3 高階の常微分方程式

3.1 4次のルンゲ・クッタ法を使う方法

ここまで示した方法は、わりとエレガントな方法である。しかし、1階の常微分方程式しか 取り扱えないので不便きわまりないと思っている者もいるだろう。一般に、高階の常微分 方程式は、1階の連立微分方程式に変形できる。このことから、高階の常微分方程 式の近似解は、これまで示した方法を用いて計算できるようになる。諸君は、1階の常微 分方程式が計算できれば、ちょっとの工夫で高階のものも計算できるのである。

重要なことは、高階の常微分方程式を1階の連立微分方程式に直すことである。まずは、 その方法を示す。例えば、次のような2階の常微分方程式があったとする。

$$\frac{\mathrm{d}^2 y}{\mathrm{d}x^2}=f\left(x,y,\frac{\mathrm{d}y}{\mathrm{d}x}\right)$$ (29)

この方程式の右辺は、 $(x, y, \mathrm{d}y/\mathrm{d}x)$の3つの関数に見えるが、実際には独立 変数は$x$のみである。$y$も、 $\mathrm{d}y/\mathrm{d}x$も$x$の関数となっている。

この2階常微分方程式を1階の連立微分方程式にするために、

$$\left\{ \begin{aligned}Y_0(x)&=y(x)\\ Y_1(x)&=y^{\prime}(x)\\ \end{aligned} \right.$$

のように変数変換をする。すると、式(29)は

$$\left\{ \begin{aligned}\frac{\mathrm{d}Y_0}{\mathrm{d}x}&=Y_1\\... ...c{\mathrm{d}Y_1}{\mathrm{d}x}&=f(x,Y_0,Y_1) \end{aligned} \right.$$

と変形できる。これで、2階の常微分方程式が1階連立常微分方程式に変換されたことにな る。1階の微分方程式ということで、4次のルンゲ・クッタ法が使える。次のようにすれば よい。

$$\left\{ \begin{aligned}k_1&=hY_{1\_n}\\ \ell_1&=hf(x_n,Y_{0\_n}... ...+\frac{1}{6}(\ell_1+2\ell_2+2\ell_3+\ell_4) \end{aligned} \right.$$

この漸化式を芋づる式に計算すれば、元の2階の微分方程式の近似解が求められるわけで ある。近似解$y(x)$は$Y_{0\_i}$となり、その微分も同時に計算され$Y_{1\_i}$であ る。

3.2 練習問題

以下の高解常微分方程式を連立1階微分方程式に書き換えなさい。

$$(1) \hspace{2mm} y^{\prime\prime}+3y^{\prime}+5y=0 \hspace{30mm} (2) \hspace{2mm} y^{\prime\prime}+6y^{\prime}+y=0$$

$$(3) 5y^{\prime\prime}+2xy^{\prime}+3y=0 (4) y^{\prime\prime\prime}+y^{\prime}+xy=0$$

$$(5) 5y^{\prime\prime}+y^{\prime}+y=\sin(\omega x) (6) xy^{\prime\prime}+y^{\prime}+y=e^{x}$$

$$(7) 5y^{\prime\prime}y^{\prime}+y^{\prime}+y=0 (8) y^{\prime\prime}y^{\prime}+x^2y^{\prime}y+y=0$$

ホームページ: Yamamoto's laboratory
著者: 山本昌志