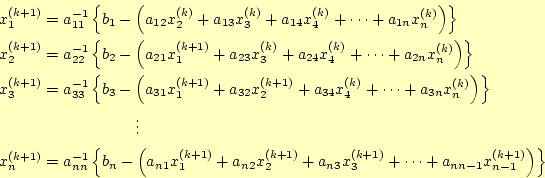2 連立一次方程式(反復法)

実用的なプログラムでは，非常に大きな連立方程式を計算しなくてはならない．数百万元 に及ぶことも珍しくない．これを，ガウス・ジョルダン法で 計算するの時間的にほとんど不可能である．そこで，これよりは格段に計算の速い方法が 用いられる．ここでは，その一つとして反復法を簡単に説明する．

当然ここでも，連立方程式

$$\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b}$$ (1)

を満たす $\boldsymbol{x}$ を数値計算により，求めることになる．ここで，真の解 $\boldsymbol{x}$ とする．

ここで，ある計算によりn回目で求められたものを $\boldsymbol{x}_n$ とする．そして，計算回数を増やして，

$$\lim_{n\rightarrow\infty}\boldsymbol{x}_n=\boldsymbol{x}$$ (2)

になったとする．この様に計算回数を増やして，真の解に近づける方法を反復法という．

この様な方法は，行列 $\boldsymbol{A}$ を $\boldsymbol{S}-\boldsymbol{T}$ と分解するだけで，容易に作ることが できる．たとえば，

$$\boldsymbol{S}\boldsymbol{x}_{k+1}=\boldsymbol{T}\boldsymbol{x}_{k}+\boldsymbol{b}$$ (3)

とすればよい．ここで， $\boldsymbol{x}_k$ が $\boldsymbol{\alpha}$ に収束するとする．すると，式 (3)と式(1)を比べれば， $\boldsymbol{\alpha}$ と $\boldsymbol{x}$ は等しいことがわかる．すなわち，式(3)で元の方程式 (1)を表した場合， $\boldsymbol{x}_k$ が収束すれば，必ず真の解 $\boldsymbol{x}$ に収束するのである．別の解に収束することはなく，真の解に収束するか，発散 するかのいずれかである．

2.1 ヤコビ法

係数行列 $\boldsymbol{A}$ の対角行列を反復計算の行列 $\boldsymbol{S}$ としたものがヤコビ(Jacobi)法で ある．係数行列を

$$\left[ \begin{array}{@{\,}ccccc@{\,}} a_{11} & a_{12} & a_{13} & ... ... & \ddots & \vdots \\ a_{n1} & a_{n2} & a_{n3} & \ldots & 0 \end{array} \right]$$ (4)

と分解し，右辺第1項が行列 $\boldsymbol{S}$ で第2項が $-\boldsymbol{T}$ となる． $\boldsymbol{x}_{k+1}$ の解の 計算に必要な $\boldsymbol{S}$ の逆行列は，それが対角行列なので，

$$\boldsymbol{S}^{-1}= \left[ \begin{array}{@{\,}ccccc@{\,}} a_{11}... ...vdots & \ddots & \vdots \\ 0 & 0 & 0 & \ldots & a_{nn}^{-1} \end{array} \right]$$ (5)

と簡単に求めることができる．$k+1$ 番目の近似解は $\boldsymbol{x}_{k+1}=\boldsymbol{S}^{-1}\left(\boldsymbol{b}+\boldsymbol{T}\boldsymbol{x}_k\right)$ となるなので，容易に 求めることができる．実際，$k$ 番目の解を

$$x_1^{(k)},\,x_2^{(k)},\,x_3^{(k)},\,\cdots,\,x_n^{(k)}$$

とすると，k+1番目の解は

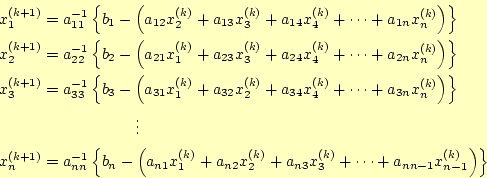$$\begin{align*}\begin{aligned}&x_1^{(k+1)}=a_{11}^{-1}\left\{b_1-\left( a_{12}x_2... ...^{(k)}+ \cdots+a_{nn-1}x_{n-1}^{(k)}\right)\right\} \\ \end{aligned}\end{align*}$$ (6)

と計算できる．これを繰り返して連立方程式の解を求める方法が，ヤコビ法である．

2.2 ガウス・ザイデル法

ヤコビ法の特徴では， $\boldsymbol{x}^{(k+1)}$ の近似値は，すべてその前の値 $\boldsymbol{x}^{(k)}$ を 使うことにある．大きな行列を扱う場合，全ての $\boldsymbol{x}^{(k+1)}$ と $\boldsymbol{x}^{(k)}$ を記 憶する必要があり，大きなメモリーが必要となり問題が生じる．今では，個人で大きなメ モリーを使い計算することは許されるが，ちょっと前まではできるだけメモリーを節約し たプログラムを書かなくてはならなかった．

そこで， $\boldsymbol{x}^{(k+1)}$ の各成分の計算が終わると，それを直ちに使うことが考えば， メモリーは半分で済む．即ち，$x_i^{k+1}$ を計算するときに，

$$x_i^{k+1} =a_{ii}^{-1}\left\{b_i-( a_{i1}x_1^{(k+1)}+a_{i2}x_2^{(k+1)}+a_{i3}x_3^{(k+1)}+\cdots+ a_{ii-1}x_{i-1}^{(k+1)}+\right.$$

$$\qquad\qquad\qquad\qquad\qquad\qquad \left. a_{ii+1}x_{i+1}^{(k)}+a_{ii+2}x_{i+2}^{(k)}+a_{ii+3}x_{i+3}^{(k)}+\cdots+ a_{in}x_n^{(k)})\right\}$$ (7)

とするのである．実際の計算では，$k+1$ 番目の解は

$$\begin{align*}\begin{aligned}&x_1^{(k+1)}=a_{11}^{-1}\left\{b_1-\left( a_{12}x_2... ...k+1)}+\cdots+a_{nn-1}x_{n-1}^{(k+1)}\right)\right\} \\ \end{aligned}\end{align*}$$ (8)

と計算できる．これを繰り返して連立方程式の解を求める方法が，ガウス・ザイデル法である．

2.3 SOR法

ガウス・ザイデル法をもっと改善する方法がある．ガウス・ザイデル法の解の修正は， $x_{k+1}-x_k$ であったが，これをもっと大きなステップにしようというのである．通常 の場合，ガウス・ザイデル法では近似解はいつも同じ側にあり，単調に収束する．そのた め，修正を適当にすれば，もっと早く解に近づく．修正幅を，加速緩和乗数$\omega$ を用 いて， $\omega(x_{k+1}-x_k)$ とする事が考えられた．これが，逐次加速緩和法(SOR法: Successive Over-Relaxation)である．

具体的な計算手順は，次のようにする．ここでは，ガウス・ザイデル法の式 (8)を用いて，得られた近似解を $\tilde{x}_i^{(k+1)}$ としている．

$$\begin{align*}\begin{aligned}&\tilde{x}_1^{(k+1)}=a_{11}^{-1}\left\{b_1-\left( a... ...+\omega\left(\tilde{x}_n^{(k+1)}-x_n^{(k)}\right)\\ % \end{aligned}\end{align*}$$ (9)

これを繰り返して連立方程式の解を求める方法が，SOR法である．

ここで，問題なのが加速緩和係数$\omega$ の値の選び方である．明らかに，それが1の場 合，ガウス・ザイデル法となりメリットは無い．また，1以下だと，ガウス・ザイデル法 よりも収束が遅い．ただし，ガウス・ザイデル法で収束しないような問題には使える．

従って，1以上の値にしたいわけであるが，余り大きくすると，発散するのは目に見えて いる．これについては，2を越えると発散することが分かっている．最適値となると，だ いたい1.9くらいが選ばれることが多い．

ホームページ: Yamamoto's laboratory
著者: 山本昌志