Subsections
3 補間法
実験やシミュレーションを行うと,離散的にデータが得られるのは普通である.例えば, 半導体の電圧・電圧特性の測定では,実験等を通して得られる結果は離散的であるが,実際の現象は連続的なことが多い.この 離散的な値を用いて,測定点の間の値,ここでは電流と電圧の関係を求めるのが補間法の 役割である.ここで学習したラグランジュ補間もスプライン補間も,全てのグラフ上の測 定点を通る曲線の方程式を求めている.
2次元のグラフ上の点は,数学では座標![]() の点として与えられる.以降の説明では,
電圧・電流などのように特定の問題にとらわれないよう,一般化した座標
の点として与えられる.以降の説明では,
電圧・電流などのように特定の問題にとらわれないよう,一般化した座標![]() で話
を進める.
で話
を進める.
3.1 ラグランジュ補間
平面座標上に
この性質を利用すると,![]() 個の点がある場合,
個の点がある場合,![]() 次関数で補間できることが分かる.
ラグランジュ補間とは,まさにこのことそのものである.数学の授業で,ある3点
次関数で補間できることが分かる.
ラグランジュ補間とは,まさにこのことそのものである.数学の授業で,ある3点
![]() を通る2次関数
を通る2次関数
![]() の
の![]() を求めた
ことがあると思うが,それと同じである.そこでは,それぞれの
を求めた
ことがあると思うが,それと同じである.そこでは,それぞれの![]() と
と![]() の値を代入して,
連立方程式をつくり
の値を代入して,
連立方程式をつくり![]() を求めたはずである.
を求めたはずである.
コンピューターを用いて,![]() 個の点を通る
個の点を通る![]() 次方程式を表す
次方程式を表す![]() 個の係数を連立方
程式を解くことにより求めることは可能である.しかし,最終目的の
個の係数を連立方
程式を解くことにより求めることは可能である.しかし,最終目的の![]() 次関数の値を求
めると言う意味では不経済である.補間という目的からすると,関数を形成する係数なん
か,全く興味の対象外なのである.そこで,係数が分からなくても,
次関数の値を求
めると言う意味では不経済である.補間という目的からすると,関数を形成する係数なん
か,全く興味の対象外なのである.そこで,係数が分からなくても,![]() 次関数を示すも
のとして,ラグランジュ補間が使われる.
次関数を示すも
のとして,ラグランジュ補間が使われる.
2次元座標上に![]() 個の点,
個の点,
![]() のラグランジュ補間は,
のラグランジュ補間は,
となる.
この式(10)を見ると,
- 各項の分母は定数で,分子はN次関数である.このことから,全ての項はN次関数 になっていることが理解できる.したがって,この式はN次関数(N次多項式)である.
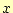 に
に
 を代入すると,
を代入すると,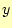 の値は
の値は
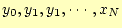 になることが分かる.これは,データ点
になることが分かる.これは,データ点
 の全てを
通過していることを示している.
の全てを
通過していることを示している.
式 (10)をもうちょっと格好良く書けば,
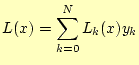 |
(11) |
ただし,
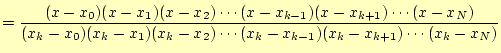 |
||
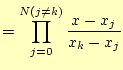 |
(12) |
となる.
ラグランジュ補間の考え方は単純で,その計算も簡単である.しかし,補間の点数が増え てくると,ラグランジュの補間には問題が生じる.ラグランジュの補間では,補間の点数 が増えてくると大きな振動が発生して,もはや補間とは言えなくなる.ラグランジュの補 間には常にこの問題が付きまうので,データ点数が多い場合は使えなくなる.
3.2 スプライン補間
3.2.1 区分多項式
ラグランジュの補間は,データ点数が増えてくると関数が振動し問題が発生する.そこで, 補間する領域をデータ間隔
補間をするデータは,先と同じように
![]() とする.そし
て,区間
とする.そし
て,区間
![]() で補間をする関数を
で補間をする関数を![]() とする.この様子を
図1に示す.
とする.この様子を
図1に示す.
3.2.2 係数が満たす式
3次のスプライン補間を考えるので,となる.スプライン補間を行う場合,この
これらの4![]() 個の未知数を決めるためには,
個の未知数を決めるためには,![]() 個の方程式が必要である.そのために,
3次のスプライン補間に以下の条件を課すことにする.
個の方程式が必要である.そのために,
3次のスプライン補間に以下の条件を課すことにする.
- 全てのデータ点を通る.各々の
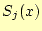 に対して両端での値が決まる
ため,2
に対して両端での値が決まる
ため,2 個の方程式ができる.
個の方程式ができる.
- 各々の区分補間式は,境界点の1次導関数は連続とする.これにより,
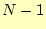 個の方程式ができる.
個の方程式ができる.
- 各々の区分補間式は,境界点の2次導関数は連続とする.これにより,
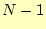 個の方程式ができる.
個の方程式ができる.
以上の条件を課すと![]() 個の方程式が決まる.未知数は4
個の方程式が決まる.未知数は4![]() 個なので,2個方程式が不
足している.この不足を補うために,いろいろな条件が考えられるが,通常は両端
個なので,2個方程式が不
足している.この不足を補うために,いろいろな条件が考えられるが,通常は両端![]() と
と![]() での2次導関数の値を0とする.すなわち,
での2次導関数の値を0とする.すなわち,
![]() である.これを自然スプラ
イン(natural spline)と言う.自然スプライン以外には,両端の1次導関数の値を指定す
るものもある.
である.これを自然スプラ
イン(natural spline)と言う.自然スプライン以外には,両端の1次導関数の値を指定す
るものもある.
これで全ての条件が決まった.あとは,この条件に満たす連立方程式を求めるだけである.
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
2006-02-08
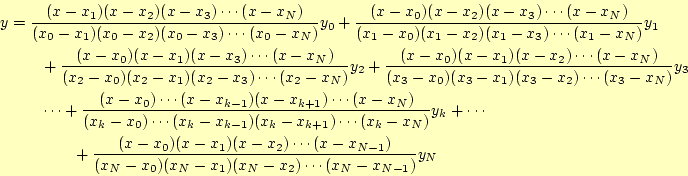
![\includegraphics[keepaspectratio,scale=0.7]{figure/Spline.eps}](img56.png)