2 前回の復習

2.1 関数の最大値

関数の最大値を探索プログラムの作成を行った．例えば，以下の関数

$$f(x)=-5x^2+6x+6\sin x -1000\leqq x \leqq 1000$$ (1)

の最大値を計算する．ただし，コンピューターでは全ての実数の範囲--負の無限大から 正の無限大まで--を取り扱うことは不可能である．そのため，範囲の指定が必要で， これが数学と異なる．コンピューターで最大値を検索する場合，図 1のように値を少しずつ変化させて，関数を計算し，最大値を探索 する．アルゴリズムは以下のようになる．

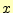1. 独立変数$x$の範囲の左端--最小値--のときを暫定最大値とする．
2. 以下を独立変数が右端--最大値--に達するまで繰り返す．
   1. 独立変数$x$の値を計算のステップ幅--リスト1の dx--分，増加させる．
   2. 再度，関数を計算する．
   3. 計算された関数の値とそれまでの最大値と比較する．もし，計算された関 数の値の方が大きいならば，以下を実行する．
      • 独立変数の最大値--リスト1の max_x--を変更する．
      • 関数の最大値--リスト1の max_fx--を変更する．
3. 独立変数の最大値と関数の最大値を表示する．

これをフローチャートにすると図2のようになる．また，リスト 1がフローチャートに従って作成したプログラムである．

図 1: 関数の最大値の検索．

図 2: 関数の最大値の検索プログラムのフローチャート．

   1 #include <stdio.h>
   2 #include <math.h>
   3 
   4 int main(void){
   5   double xmin, xmax, x, dx, fx; 
   6   double max_fx, max_x;            // 最大を格納する変数
   7   int i, ncal;
   8 
   9   xmin = -1000.0;                  // xの最小値
  10   xmax =  1000.0;                  // xの最大値
  11   dx = 0.0001;                     // xの計算のきざみ幅（誤差の程度)
  12   ncal = (xmax-xmin)/dx;           // 計算回数
  13 
  14   //--- 暫定最大 ( x=xmin を暫定最大とする) ---------
  15   x = xmin;
  16   max_x = x;
  17   max_fx = -5.0*x*x + 6.0*x + 6*sin(x);
  18 
  19   for(i=1; i<=ncal; i++){
  20     x = xmin + i*dx;                        // xの計算
  21     fx = -5.0*x*x + 6.0*x + 6*sin(x);       // f(x)の計算
  22 
  23     //---- 最大値か否かの検査 --------------
  24     if(max_fx < fx){                        // 新たに最大値発見
  25       max_x = x;
  26       max_fx = fx;
  27     }
  28 
  29   }
  30 
  31   printf("x = %fのときf(x)=%fで最大です\n", max_x, max_fx);
  32 
  33   return 0;
  34 }

2.2 連立不等式

次に連立不等式が成り立つ範囲を表示するプログラムの作成の練習を行った．例えば，次 のような連立不等式である．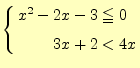

$$\left\{ \begin{aligned}x^2-2x-3&\leqq 0\\ 3x+2 &< 4x \end{aligned} \right. -1000\leqq x \leqq 1000$$ (2)

これも関数の最大値を検索するのと似た方法をつかう．独立変数$x$に値を代入して，そ の連立不等式が成り立つか否か--を範囲の左端から右端まで調べる．そして，連立不等 式が成立する値の左端から，右端の値を表示させる．図2のように である．不等式が成立しない--NG--と成立する--OK--という状態が変化したときに独 立変数$x$の値を表示させる．具体的には次のように行う．

• NGからOKに変化したときが，不等式が成立する範囲の左端である．
• OKからNGに変化したときが，不等式が成立する範囲の右端である．

これを実現するためには，現在とその直前の状態を示す2つの変数--リスト 2のpreとnow--が必要である．これら2つを比較して，状態 の変化を調べる．

具体的なアルゴリズムは以下のようにする．

1. 初期値を決める．調べる独立変数の前の状態--リスト2の pre--を「NG」とする．
2. 以下を独立変数が右端--最大値--に達するまで繰り返す．
   1. 変数の値を計算のステップ幅分，増加させる．
   2. 再度，連立不等式を計算して，現在の状態--リスト2の pre--を設定する．
   3. 現在の状態と直前の状態を比較して，それが変化しているならば以下を実 行する．
      • NGからOKに変化したならば，「現在の独立変数の値--から」と表示する．
      • OKからNGに変化したならば，「現在の独立変数の直前の値--まで」と表 示する．
3. 最後の値--独立変数の右端--の処理．最後の状態がOKならば，「現在の独立変 数の値--まで」と表示する．

図 3: 連立不等式の計算．

   1 #include <stdio.h>
   2 
   3 int main(void){
   4   double xmin, xmax, x, dx; 
   5   int pre , now;
   6   int i, ncal;
   7   
   8   xmin = -1000.0;                  // xの最小値
   9   xmax =  1000.0;                  // xの最大値
  10   dx = 0.0001;                     // xの計算のきざみ幅（誤差の程度)
  11   ncal = (xmax-xmin)/dx;           // 計算回数
  12 
  13   printf("連立不等式が成立するのは以下の範囲です\n");
  14 
  15   pre = 0;
  16 
  17   for(i=1; i<=ncal; i++){
  18     x = xmin + i*dx;               // 検査する x
  19 
  20     // --- 連立不等式が OK or NG の検査 ----
  21     if(x*x-2*x-3 <= 0 && 3*x+2 < 4*x){
  22       now = 1;                     // OKの場合
  23     }else{
  24       now = 0;                    // NGの場合
  25     }
  26 
  27     // --- OK と NG の境界の処理 ----
  28     if(now != pre){
  29       if(now == 1){
  30 	printf("%fから\t", x);
  31       }else{
  32 	printf("%fまで\n", x-dx);
  33       }
  34     }
  35 
  36     pre = now;
  37   }
  38 
  39   if(now == 1){                     // 最後がOKのときの処理
  40     printf("%fまで\n", x);
  41   }
  42 
  43   return 0;
  44 }

ホームページ: Yamamoto's laboratory
著者: 山本昌志