6 2進数を用いた小数の表現

6.1 位取り記数法

10進数での小数の表現を考える．例えば，次の小数は

$$(0.1235)_{10} =(1\times 10^{-1}+2\times 10^{-2}+3\times 10^{-3}+5\times 10^{-4})_{10}$$ (16)

となっており，整数の場合と同じである．小数点を境に，右側の指数部が-1, -2, -3と1ず つ減少する．これは，先に示した整数の場合と全く同じで，簡単である．当然，

$$10^{-1}=\frac{1}{10^1}=\frac{1}{10}=0.1$$

$$10^{-2}=\frac{1}{10^2}=\frac{1}{100}=0.01$$

$$10^{-3}=\frac{1}{10^3}=\frac{1}{1000}=0.001$$

$$\qquad\vdots$$

$$10^{-N}=\frac{1}{10^N}$$ (17)

は理解していなくてはならない．

6.2 基数の変換(2進数 $\rightarrow$10進数)

2進数での少数の表記も，10進数の場合と同じである．だから，2進数少数を10進数少数に 変換するのは簡単である．たとえば，

$$(0.10101)_2 =(1\times 10^{-1}+0\times 10^{-10}+1\times 10^{-11}+ 0\times 10^{-100}+1\times 10^{-101})_2$$

$$=(1\times 2^{-1}+0\times 2^{-2}+1\times 2^{-3}+ 0\times 2^{-4}+1\times 2^{-5})_{10}$$

$$=(1\times 0.5+0\times 0.25+1\times 0.125+ 0\times 0.0625+1\times 0.03125)_{10}$$

$$=(0.5+0.125+0.03125)_{10}$$

$$=(0.65625)_{10}$$ (18)

となる．当然

$$2^{-1}=\frac{1}{2^1}=\frac{1}{2}=0.5$$

$$2^{-2}=\frac{1}{2^2}=\frac{1}{4}=0.25$$

$$2^{-3}=\frac{1}{2^3}=\frac{1}{8}=0.125$$

$$\qquad\vdots$$

$$2^{-N}=\frac{1}{2^N}$$ (19)

は理解していなくてはならない．

6.3 基数の変換(10進数 $\rightarrow$2進数)

つぎは，先ほどと逆を考える．たとえば，先ほどの例の $(0.65625)_{10}$を2進数で表現 する．そのためには，

$$(0.65625)_{10} =(a_1\times 2^{-1}+a_2\times 2^{-2}+a_3\times 2^{-3}+\cdots)_{10}$$ (20)

と書き直せばよい．ただし，$a_n$は0または1である．そして，この$a_n$を並べると，

$$(0.65625)_{10}=(a_1a_2a_3a_4\cdots)_2$$ (21)

と2進数で表現できる．ここで，問題は$a_n$を求めることである．そこで，式 (20)の両辺を2倍する．すると，

$$(1.3125)_{10} =(a_1\times 2^{0}+a_2\times 2^{-1}+a_3\times 2^{-2}+\cdots)_{10}$$ (22)

となる．この式の両辺の整数部と小数部は等しいので，

$$(1)_{10}=(a_1)_{10} (0.3125)_{10} =(a_1\times 2^{0}+a_2\times 2^{-1}+a_3\times 2^{-2}+\cdots)_{10}$$ (23)

となる．これで，$a_1=1$が求まった．同じように，残りの小数部分を2倍すると，

$$(0.625)_{10} =(a_2\times 2^{0}+a_3\times 2^{-1}+a_4\times 2^{-2}+\cdots)_{10}$$ (24)

となる．これも，両辺の整数部と小数部が等しいので，

$$(0)_{10}=(a_2)_{10} (0.625)_10=(a_3\times 2^{-1}+a_4\times 2^{-2}+a_5\times 2^{-3}+\cdots)_{10}$$ (25)

が得られる．これで，$a_2=0$が求まった．同様に以下の通り，残りの小数部分の計算を進める と，全ての$a_n$が求まる．

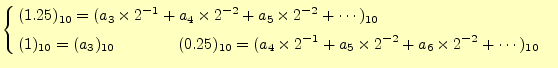$$\left\{ \begin{aligned}&(1.25)_{10} =(a_3\times 2^{-1}+a_4\times ... ...es 2^{-1}+a_5\times 2^{-2}+a_6\times 2^{-2}+\cdots)_{10}& \end{aligned} \right.$$ (26)

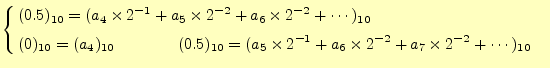$$\left\{ \begin{aligned}&(0.5)_{10} =(a_4\times 2^{-1}+a_5\times 2... ...es 2^{-1}+a_6\times 2^{-2}+a_7\times 2^{-2}+\cdots)_{10}& \end{aligned} \right.$$ (27)

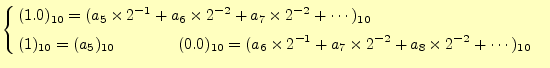$$\left\{ \begin{aligned}&(1.0)_{10} =(a_5\times 2^{-1}+a_6\times 2... ...es 2^{-1}+a_7\times 2^{-2}+a_8\times 2^{-2}+\cdots)_{10}& \end{aligned} \right.$$ (28)

最後に，小数部がゼロとなったので計算は，完了となる．以上をまとめると

$$(0.65625)_{10} =(a_1\times 2^{-1}+a_2\times 2^{-2}+a_3\times 2^{-3}+\cdots)_{10}$$

$$=(1\times 2^{-1}+0\times 2^{-2}+1\times 2^{-3}+0\times 2^{-4}+1\times 2^{-5}+)_{10}$$

$$=(0.10101)_2$$ (29)

となる．要するに，小数部を2倍して，その整数部を書いていけばよい．

普通は，図7のようにして計算を進める．2倍して，整数部を書き出して， 小数部を再度2倍する．これを繰り返すと，10進数小数を2進数小数に変換することができ る．10進数の0.1は循環小数ではないが，2進数にすると，

$$(0.1)_{10}=(0.00011001100110011\cdots)_2$$ (30)

と循環小数になる．通常は，途中まで(必要な精度まで)で計算を打ち切る．

図 7: 小数の基数変換(10進数 $\rightarrow$2進数)

ホームページ: Yamamoto's laboratory
著者: 山本昌志