7 コンピューター内部での正の整数以外の表現

これは少しレベルの高い内容で，もう少し時間をかけないと説明できない．将来，情報関 係の仕事に就きたい者，あるいは自分の能力に自信のある者は独力で以下の内容を理解せ よ．非常におもしろい内容であるはずである．

7.1 負の整数の表現

普通のC言語の整数型(int)は，4バイト(32ビット)であるが，ここでは図を簡単にす るため，16ビットで説明する．32ビットでも同じである．

負の整数は，補数(complement)を使って，コンピューター内部では表現される．それを図 8に示すが，手順は，次の通りである． -4pt

1. 絶対値を2進数のビットパターンで表現し，その反転を行う．
2. 反転されたビットパターンに1を加算する．

このようにしてできたビットパターンをメモリーに記憶させ，それを負の数として取り扱 う．

図 8: 負の整数をメモリーに格納する方法

この方法のメリットは，減算が加算器でできることである．補数表現のイメージは， 図9の通りである．車の距離計に似ている．

図 9: 距離計イメージ(2の補数表示)

それでは，なぜ，補数表現だと，減算が加算器で可能なのだろうか?．減算の演算は，負 の数の加算と同じである．したがって，図9のように負の数を 表現すると，負の整数の加算は正の整数の加算と同じと分かるであろう．したがって，加 算器で減算が可能となる．実際，正の数の減算を行うときは，ビットの反転と+1加算を実 施して，加算器で計算する．イメージは，図9の通りであるが， もう少し，理論的に説明をおこなうとしよう．ある正の整数を$x$とする．その負の数，$-x$ は補数表現では，

$$[-x]=(FFFF-x+1)_{16}$$ (31)

となる．左辺の$[-x]$が$-x$の意味である．$[\quad]$の意味は，括弧内の負の整数を計 算機内部の表現を表している．これは，私が作った表記なので，一般には用いられていな い．右辺の$FFFF-x$がビット反転になっている．ここでは，16ビットで整数を表現しよう としているので，$FFFF$から$x$を引いてビット反転させている．疑問に思う者は実際に 計算して見よ．それに1を加えて，補数の表現としている．つぎに，ある整数$y$を考えて， $y-x$を計算してみよう．

$$[y-x]=(y+FFFF-x+1)_{16}$$ (32)

$FFFF-x+1$は，あらかじめ計算されて，コンピューター内部のメモリーに格納されている ので，$[y-x]$は加算器で可能である．これは，あたりまえです．重要なことは，この結 果が，負の場合，2の補数表現になっており，正の場合，そのままの値になっていること である．

演算の結果，$y-x$が負になる場合を考えよう．すると式(32)は，

$$[y-x]=(FFFF-(x-y)+1)_{16}$$ (33)

と変形できる．この場合，絶対値が $(x-y)$ なので，絶対値のビット反転と+1加算となっ ていることが理解できる．つぎに，$y-x$が正になる場合を考えましょう．すると式(32)は，

$$[y-x] =(y-x+FFFF+1)_{16}$$

$$=(y-x+10000)_{16}$$ (34)

となる．10000は計算機内部では，桁上がりを示す．16ビットの表示では無視される．し たがって，内部の表現は，正しく表せる．

コーヒーブレイク この方法で負の数を表すことは，1970年頃には常識となったようである．驚いたことに，負 の数をこの補数で表すアイディアは，パスカルが最初です．パスカルは，パスカリーヌと いう歯車式計算機を1642年頃に製作しています．そこの減算を加算器で行うために，補数 というものを考えたようです．

7.1.1 ビット反転と+1加算の意味

$x$を正の整数として，$-x$をコンピューターの内部で表現する場合， -4pt

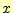1. $x$をビット反転する．
2. +1加算する．

の操作で得られたものその内部表現になる．式で表すと，

$$[-x]=(FFFF-x+1)_{16}$$ (35)

である．この操作の意味を調べてみよう．結論から言 うと，この操作は符号反転(-1乗算)の操作になっている．それを示すために，もう一度こ の操作を繰り返してみる．すると，

$$\left\{FFFF-(FFFF-x+1)+1\right\}_{16} =(x)_{16}$$

$$=[x]$$ (36)

となる．このことから，この操作は，符号反転であることが理解できる．式 (35)は，$x$の符号反転を示しており，式(36) は$-x$の符号反転を示している．

式(35)は，-xのコンピューターの内部表現を表している．従って，元の xを求めるためには，その逆の操作 -4pt

1. 1減算(-1加算)する．
2. ビット反転する．

をすればよく，式だと

$$\left[FFFF-\left\{(FFFF-x+1)-1\right\}\right] =(x)_{16}$$

$$=[x]$$ (37)

となる．しかし，元の表現を得るためには，式(36)の演算でも良 いはずである．式(37)を変形すると，容易に式 (36)を導くことができる．これらのことから，以下の結論を導く ことができる． -4pt

• ビット反転と+1加算の操作は，整数のコンピューターの内部での表現の符号反転で ある．
• この符号反転の反対の操作である1減算とビット反転の操作は，ビット反転と1加 算と同じ操作である．

7.2 浮動小数点表示

実際のコンピューターを用いた計算では，実数がよく使われる．ここでは，C言語の倍精 度実数型「double」で変数を宣言したときの，データの格納の仕方を示す．

7.2.1 浮動小数点表示とは

浮動小数点表示とは，指数化（例えば， $-0.123\times 10^{-2}$）して数値を表現する． これは非常に便利な方法で，自然科学では多くつかわれる．コンピューターでも同様で， データが整数と指定されない限りこの浮動小数点が用いられる．実際，この仮数部の (-0.123)と指数の(-2)をメモリーに格納する．この方法の長所と短所は，以下の通りであ る．

-4pt

長所

決められたビット数内で，非常に小さな数値から大きな数値まで表現可能になる．

短所

桁落ち誤差が発生する場合がある．

浮動小数点表示を学習するために，必要な言葉の意味は，図10の 通りである．1年生の数学の授業で学習したはず．

図 10: 指数表現の名称

7.2.2 C言語の倍精度実数型

IEEEの規格のC言語の倍精度実数型の「double」の表現について説明する．まず，浮動小数点 表示のための正規化を図11に示す．当然，仮数部，指数部とも2 進数表現である．仮数部は，符号と1.XXXXのように表す．

図 11: IEEE規格表現のための規格化

つぎに，これをIEEE規格の浮動小数点に表すことを考える．まずその規格の仕様は，以下 のようになっている． -4pt

• 64ビット(第0ビット〜第63ビット)で，浮動小数を表わす．各ビットの構成は，図 12の通りである．
• 最上位の第63ビットが仮数部の符号ビットである．正の場合ゼロで，負の場合1に なる．
• 指数は11ビットでオフセットバイナリ方式で表す．11ビットで0〜2047の値に なる．ただし，指数部11ビットの値0と2047は例外処理のために予約されてい る．11ビットで表現される値からオフセット値1023を引くことにより指数の値が -1022〜1023の範囲になるように定められている．
• 仮数部は52ビットである．小数点以下を，絶対値で表現する．規格化のための整数 部は1と分かっているので，このためのビットは割り当てられていない．

図 12: IEEE規格(C言語の倍精度実数)表現のビットの内訳

以上の仕様をもとに，図11で規格化された数を浮動小数点表示を 示す．ほとんどの部分は規格化で分かるが，指数のみ計算が必要である．指数は，オフセッ トバイナリーで計算するために，まず10進数で表す．

$$(-1011)_2=(-8-2-1)_{10}=(-11)_{10}$$ (38)

不動小数表示の指数は，この式の値に 1023 を加算して求める．すると，

$$(-11+1023)_{10}=(1012)_{10}=(1111110100)_2$$ (39)

となる．

これで，すべて準備が整った．不動小数点表示は，図13のようにな る．実際のコンピューターには，この64ビットのデータが格納される．メモリーは８ビッ ト(1バイト)毎アドレスが割り当てられているので，8番地分のデータ領域が必要である．

図 13: IEEE規格の浮動小数点表示の例

ホームページ: Yamamoto's laboratory
著者: 山本昌志