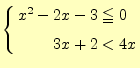4 プログラム例

4.1 1〜1000までの和の計算プログラム

3つの繰り返し文を使った1〜1000までの和を計算するプログラムを，リスト 1-に示す．

   1 #include <stdio.h>
   2 
   3 int main(void){
   4   int i, sum;
   5 
   6   sum=0;
   7   i=1;
   8 
   9   while(i<=1000){
  10     sum += i;
  11     i++;
  12   }
  13  
  14   printf("1から1000までの和は，%dです．\n", sum);
  15 
  16   return 0;
  17 }

   1 #include <stdio.h>
   2 
   3 int main(void){
   4   int i, sum;
   5 
   6   sum=0;
   7 
   8   for(i=1; i<=1000; i++){
   9     sum += i;
  10   }
  11  
  12   printf("1から1000までの和は，%dです．\n", sum);
  13 
  14   return 0;
  15 }

   1 #include <stdio.h>
   2 
   3 int main(void){
   4   int i, sum;
   5 
   6   sum=0;
   7   i=1;
   8 
   9   do{
  10     sum += i;
  11     i++;
  12   }while(i<=1000);
  13  
  14   printf("1から1000までの和は，%dです．\n", sum);
  15 
  16   return 0;
  17 }

4.2 最大値を求めるプログラム

リスト4は，関数

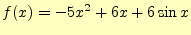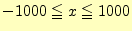$$f(x)=-5x^2+6x+6\sin x -1000\leqq x \leqq 1000$$ (1)

の最大値を計算するプログラムである．計算のステップ幅--計算精度を表す-- は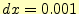，$dx=0.001$ としている．すなわち，

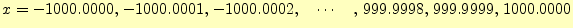$$x=-1000.0000,\,-1000.0001,\,-1000.0002,\quad\cdots\quad,\,999.9998,\,999.9999,\,1000.0000$$ (2)

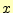と$x$の値を変化させて，関数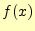$f(x)$の値を計算している．

   1 #include <stdio.h>
   2 #include <math.h>
   3 
   4 int main(void){
   5   double xmin, xmax, x, dx, fx; 
   6   double max_fx, max_x;            // 最大を格納する変数
   7   int i, ncal;
   8 
   9   xmin = -1000.0;                  // xの最小値
  10   xmax =  1000.0;                  // xの最大値
  11   dx = 0.0001;                     // xの計算のきざみ幅（誤差の程度)
  12   ncal = (xmax-xmin)/dx;           // 計算回数
  13 
  14   //--- 暫定最大 ( x=xmin を暫定最大とする) ---------
  15   x = xmin;
  16   max_x = x;
  17   max_fx = -5.0*x*x + 6.0*x + 6*sin(x);
  18 
  19   for(i=1; i<=ncal; i++){
  20     x = xmin + i*dx;                        // xの計算
  21     fx = -5.0*x*x + 6.0*x + 6*sin(x);       // f(x)の計算
  22 
  23     //---- 最大値か否かの検査 --------------
  24     if(max_fx < fx){                        // 新たに最大値発見
  25       max_fx = fx;
  26       max_x = x;
  27     }
  28 
  29   }
  30 
  31   printf("x = %fのときf(x)=%fで最大です\n", max_x, max_fx);
  32 
  33   return 0;
  34 }

4.3 連立不等式

リスト5は，基礎数学の教科書p.62の練習問題2-Aの2.(2)の連立不等 式

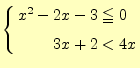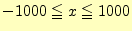$$\left\{ \begin{aligned}x^2-2x-3&\leqq 0\\ 3x+2 &< 4x \end{aligned} \right. -1000\leqq x \leqq 1000$$ (3)

を計算するプログラムである．計算のステップ幅--計算精度を表す-- は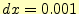，$dx=0.001$としている．

   1 #include <stdio.h>
   2 
   3 int main(void){
   4   double xmin, xmax, x, dx; 
   5   int period , current;
   6   int i, ncal;
   7   
   8   xmin = -1000.0;                  // xの最小値
   9   xmax =  1000.0;                  // xの最大値
  10   dx = 0.0001;                     // xの計算のきざみ幅（誤差の程度)
  11   ncal = (xmax-xmin)/dx;           // 計算回数
  12 
  13   printf("連立不等式が成立するのは以下の範囲です\n");
  14 
  15   period = 0;
  16 
  17   for(i=1; i<=ncal; i++){
  18     x = xmin + i*dx;               // 検査する x
  19 
  20     // --- 連立不等式が OK or NG の検査 ----
  21     if(x*x-2*x-3 <= 0 && 3*x+2 < 4*x){
  22       current = 1;                 // OKの場合
  23     }else{
  24       current = 0;                 // NGの場合
  25     }
  26 
  27     // --- OK と NG の境界の処理 ----
  28     if(current != period){
  29       if(current == 1){
  30 	printf("%f\tから\t", x);
  31 	period = current;
  32       }else{
  33 	printf("%f\n", x);
  34 	period = current;
  35       }
  36     }
  37   }
  38 
  39   return 0;
  40 }

ホームページ: Yamamoto's laboratory
著者: 山本昌志