2 区分的に連続

2.1 不連続部分の値

区分的に連続ということを考える前に，不連続部分でのフーリエ級数の値について考え る．一般的な話は難しいので，具体的な以下の関数を考えることにする．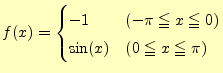

$$f(x)=\begin{cases}-1 & (-\pi\leqq x \leqq 0)\\ \sin(x) & (0\leqq x \leqq \pi) \end{cases}$$ (1)

付録Aに示すように，このフーリエ級数は，

$$f(x)=\frac{2-\pi}{2\pi}+\left(\frac{2}{\pi}+\frac{1}{2}\right)\si... ...y\left[ \frac{1+(-1)^n}{\pi(1-n^2)}\cos nx+\frac{1-(-1)^n}{n\pi}\sin nx \right]$$ (2)

となる．これを$n=10000$まで，コンピューターにより計算した結果を図1 に示す．

ここで，不連続点$x=0$での$f(x)$の値を考える．式(2)に代 入すると，

$$f(0) =\frac{2-\pi}{2\pi}+\sum_{n=2}^\infty\frac{1+(-1)^n}{\pi(1-n^2)}$$

$$=-\frac{1}{2}+\frac{1}{\pi}+\frac{1}{\pi}\sum_{n=2}^\infty\frac{1+(-1)^n}{1-n^2}$$

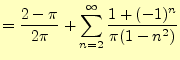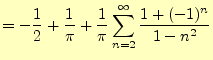$$=-\frac{1}{2}+\frac{1}{\pi}\left[1+\sum_{n=2}^\infty\frac{1+(-1)^n}{1-n^2}\right]$$

$$=-\frac{1}{2}+\frac{1}{\pi}\left[1+\left( \frac{2}{1-2^2}+\frac{2}{1-4^2}+\frac{2}{1-6^2}+\frac{2}{1-8^2}+\cdots \right)\right]$$

$$=-\frac{1}{2}+\frac{1}{\pi}\left[1+\sum_{n=1}^\infty\frac{2}{1-(2n)^2}\right]$$

$$=-\frac{1}{2}+\frac{1}{\pi}\left[ 1+\sum_{n=1}^\infty\left\{\frac{1}{1-(2n)}+\frac{1}{1+(2n)}\right\} \right]$$

$$=-\frac{1}{2}+\frac{1}{\pi}\left[ 1+\frac{1}{-1}+\frac{1}{3}+\fra... ...}+\frac{1}{5} +\frac{1}{-5}+\frac{1}{7}+\frac{1}{-7}+\frac{1}{9}+\cdots \right]$$

$$=-\frac{1}{2}$$ (3)

となる．これは，何を表しているか?．不連続点では，その両端での相加平均となってい ることを表している．この例では，左から$x=0$に近づく場合は$f(0-0)=-1$，右から近づ く場合は$f(0+0)=0$となり，$x=0$では相加平均となっている．

$$f(0)=\frac{1}{2}\left[f(0+0)+f(0-0)\right]$$ (4)

不連続点を含む関数をフーリエ級数で表した場合，$x=p$の不 連続点での値は

$$f(p)=\frac{1}{2}\left[f(p-0)+f(p+0)\right]$$ (5)

となる．

図: $f(x)=-1\quad (-\pi\leqq x \leqq 0)$, $f(x)=\sin x\quad (0\leqq x \leqq \pi)$を10000項までフーリエ級数を計算した結果．

物言い    「たしかに，この例では不連続点での値は両端の相加平均となっ ている．それが一般的に成り立つか保証はあるのか?」．なかなか，良い指摘である．こ の証明をこの講義でする時間はない．さらに，いろいろなことを学ばないとそれが理解で きないであろう．したがって，直感的には正しそうなので，そんなものと思ってほしい． 事実，不連続点での値はこれで正しいのである．納得できなければ，各自，数学の教科書 を調べよ．

このように不連続部分でも値がちゃんと存在することは重要である．有限区間で定義され た関数$f(x)$が不連続部分や関数の両端で値があるとき，その関数は区分的に連続 という．

2.2 項別微分と項別積分

フーリエ級数の両辺を微分しても積分しても，その等号の関係は成り立つ．とくに，三角 関数の和の部分は項別に微分や積分ができる．これはいままで計算した普通の関数と同じ である．
ホームページ: Yamamoto's laboratory
著者: 山本昌志