3 パーセバルの等式

3.1 証明

これまで学習したように，区間$[-L,L]$で定義された区分的に連続な関数$f(x)$は，

$$f(x) =\frac{a_0}{2} +\sum_{n=1}^{\infty}\left[ a_n\cos \frac{n\pi x}{L} +b_n\sin \frac{n\pi x}{L} \right]$$ (6)

$$\quad a_n=\frac{1}{L}\int_{-L}^{L}f(x)\cos \frac{n\pi x}{L} \,\ma... ...qquad \quad b_n=\frac{1}{L}\int_{-L}^{L}f(x)\sin \frac{n\pi x}{L} \,\mathrm{d}x$$

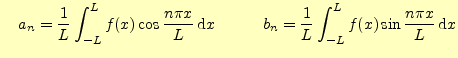のようにフーリエ級数で表すことができる．式(6)の両辺に $f(x)$を乗じて²，関数が定 義されている区間で積分を行う³．

$$\int_{-L}^{L}\left[f(x)\right]^2\,\mathrm{d}x =\int_{-L}^{L}\frac{a_0}{2}f(x)\,\mathrm{d}x +\int_{-L}^{L}\sum_{... ...eft[ a_n\cos \frac{n\pi x}{L}+b_n\sin \frac{n\pi x}{L} \right]f(x)\,\mathrm{d}x$$

$$=\frac{a_0}{2}\int_{-L}^{L}f(x)\,\mathrm{d}x +\sum_{n=1}^{\infty}... ...L}\,\mathrm{d}x +b_n\int_{-L}^{L}f(x)\sin \frac{n\pi x}{L}\,\mathrm{d}x \right]$$

$$a_n b_n$$

$$=L\frac{a_0^2}{2}+\sum_{n=1}^{\infty}\left(La_n^2+Lb_n^2\right)$$ (7)

以上より，

$$\frac{1}{L}\int_{-L}^{L}\left[f(x)\right]^2\,\mathrm{d}x =\frac{a_0^2}{2}+\sum_{n=1}^{\infty}\left(a_n^2+b_n^2\right)$$ (8)

が得られる．これをパーセバルの等式と言う．

諸君は，「計算結果は分かった．この計算結果にどんな意味があるの???」と言いたいだろう．パーセバルの等式が重要な理由は，節を変えて述べる事にする．

3.2 パーセバルの等式の意味

「パーセバルの等式は関数を展開するときのピタゴラスの定理(三平方の定理)である」と言ったら驚くであろう．これからこのことを示す．これから述べることの計算なんかどうでもよいから，イメージを持つことに努めよ．

3.2.1 ベクトルの場合のピタゴラスの定理

図2のように，ある任意のベクトルは$x$と$y$，$z$方向に分解できる． 分解されたそれぞれのベクトルは，各方向の単位ベクトルの$a$倍や$b$倍，あるいは$c$ 倍というように表現できる．すなわち，

$$\boldsymbol{X}=a\boldsymbol{i}+b\boldsymbol{j}+c\boldsymbol{k}$$ (9)

である．ここで， $\boldsymbol{i}$は$x$方向の単位ベクトル， $\boldsymbol{j}$は$y$方向の単位ベクトル， $\boldsymbol{k}$は$z$方向の単位ベクトルである．これは，ベクトル $\boldsymbol{X}$を単位ベクトル $(\boldsymbol{i},\,\boldsymbol{j},\,\boldsymbol{k})$で展開しているのである．その展開の係数が $(a,\,b,\,c)$で，それぞれの単位ベクトルの寄与を表す．これを，

$$\boldsymbol{X}=(a,\,b,\,c)$$ (10)

と表すことが多い．，線形代数では

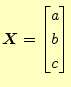$$\boldsymbol{X}=\begin{bmatrix}a\\ b\\ c \end{bmatrix}$$ (11)

のように表現したりもする．

この式をつかって自分自身の内積を計算する．左辺は $\boldsymbol{X}\cdot\boldsymbol{X}=\vert\boldsymbol{X}\vert^2$となり，ベクトルの大きさの二乗--長さの二乗--である．右辺も計算すると，次のようになる．

$$\vert\boldsymbol{X}\vert^2 =(a\boldsymbol{i}+b\boldsymbol{j}+c\boldsymbol{k})\cdot(a\boldsymbol{i}+b\boldsymbol{j}+c\boldsymbol{k})$$

$$=a^2(\boldsymbol{i}\cdot\boldsymbol{i})+ab(\boldsymbol{i}\cdot\bo... ...})+cb(\boldsymbol{k}\cdot\boldsymbol{j})+c^2(\boldsymbol{k}\cdot\boldsymbol{k})$$

$$(\boldsymbol{i}\cdot\boldsymbol{i})=(\boldsymbol{i}\cdot\boldsymbol{i})=(\boldsymbol{i}\cdot\boldsymbol{i})=1 (\boldsymbol{i}\cdot\boldsymbol{j})=(\boldsymbol{j}\cdot\boldsymbol{k})=(\boldsymbol{k}\cdot\boldsymbol{i})=0$$

$$=a^2+b^2+c^2$$ (12)

これは，まさにピタゴラスの定理である．

注意ここではめんどくさい計算を行ったが，普通は次のようにする．

$$\vert\boldsymbol{X}\vert^2=(a,\,b,\,c)\cdot(a,\,b,\,c)=a^2+b^2+c^2$$ (13)

あるいはもう少し線形代数の規則に従うと

$$\vert\boldsymbol{X}\vert^2=\begin{bmatrix}a & b& c \end{bmatrix} \begin{bmatrix}a \\ b \\ c \end{bmatrix} =a^2+b^2+c^2$$ (14)

とする．どっちでもいい．

図 2: 3次元のベクトルを単位ベクトルで分解

3.2.2 関数のピタゴラスの定理

「関数のピタゴラスの定理」という言葉は無いが，イメージをつかむために，ここではあえて使う⁴．

3.2.2.1 準備

先ほどのピタゴラスの定理を示すときに，ベクトル $\boldsymbol{X}$を単位ベクトル $(\boldsymbol{i},\,\boldsymbol{j},\,\boldsymbol{k})$で展開⁵した．それぞれの単位ベクトルの強度を示すものが係数の $(a,\,b,\,c)$である．同様に，フーリエ級数では，関数$f(x)$を $\{1,\,\cos(\pi x/L),\,\cos(2\pi x/L),\cdots,\,\sin(\pi x/L),\,\sin(2\pi x/L),\cdots\}$で展開⁶した．展開に用いた三角関のそれぞれの強度は，係数 $(a_0/2,\,a_1,\,a_2,\dots,b_1,\,b_2,\cdots)$が示すことになる．

つぎに，ベクトルの内積の演算に対応する関数の演算について考える．これは以前述べたように，積分になる．

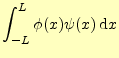$$\boldsymbol{A}\cdot\boldsymbol{B} \Rightarrow \int_{-L}^{L}\phi(x)\psi(x)\,\mathrm{d}x$$ (15)

単位ベクトルでは，次式で表せる直交性

$$(\boldsymbol{i}\cdot\boldsymbol{i})=(\boldsymbol{i}\cdot\boldsymbol{i})=(\boldsymbol{i}\cdot\boldsymbol{i})=1$$ (16)

$$(\boldsymbol{i}\cdot\boldsymbol{j})=(\boldsymbol{j}\cdot\boldsymbol{k})=(\boldsymbol{k}\cdot\boldsymbol{i})=0$$ (17)

がある．自分自身以外の内積はゼロとなっている．これに対応する三角関数の直交性は，次のようになる．

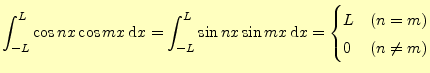$$\int_{-L}^{L}\cos nx\cos mx\,\mathrm{d}x= \int_{-L}^{L}\sin nx\sin mx\,\mathrm{d}x=\begin{cases}L & (n=m)\\ 0 & (n \ne m) \end{cases}$$ (18)

$$\int_{-L}^{L}1\times1\,\mathrm{d}x=2L$$ (19)

$$\int_{-L}^{L}\sin nx\cos mx\,\mathrm{d}x= \int_{-L}^{L}\sin nx\,\mathrm{d}x = \int_{-L}^{L}\cos nx\,\mathrm{d}x = 0$$ (20)

これもまた，自分自身以外との積分はゼロとなる．単位ベクトルとよく似ている．ただし，単位ベクトルの大きさは1であったが，展開する定数や関数の大きさは$\sqrt{2L}$あるいは$\sqrt{L}$である．

3.2.2.2 ピタゴラスの定理

準備ができたので，パーセバルの等式がピタゴラスの定理と同じであることを示す．はじめに，パーセバルの等式(8)をほんのちょっと書き直す．

$$\int_{-L}^{L}\left[f(x)\right]^2\,\mathrm{d}x =\left(\frac{\sqrt{... ...n=1}^{\infty}\left[\left(\sqrt{L}a_n\right)^2+\left(\sqrt{L}b_n\right)^2\right]$$ (21)

ピタゴラスの定理である式(12)の右辺と式(21)とは次のように対応する．

$$\vert\boldsymbol{X}\vert^2 \Rightarrow \int_{-L}^{L}\left[f(x)\right]^2\,\mathrm{d}x$$ (22)

左側は自分自身との内積，右側は自分自身との積分である．

次に右辺であるが，単位の大きさを考えなくてはならない．

• ベクトルの場合，大きさが1の単位ベクトルを基準にして，何倍という意味で係数 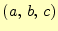$(a,\,b,\,c)$を決めた．
• 関数の場合，大きさが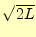$\sqrt{2L}$(定数1)あるいは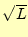$\sqrt{L}$(三角関数)を基準にして，何倍と言う意味で係数 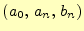$(a_0,\,a_n,\,b_n)$を決めた．

関数の方の法の単位が1と異なるため，それを1にしなくてはならない．単位を1にすると，係数は$\sqrt{2L}$あるいは$\sqrt{L}$倍する必要がある．なぜならば，「2 $\mathrm{[mm]}$単位の3倍の長さは，1 $\mathrm{[mm]}$単位の2$\times$3倍になる」からである．したがって，ベクトルと関数，それぞれ大きさが1のもので展開した場合の対応は次のようになる．

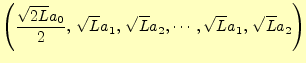$$(a,\,b,\,c) \Rightarrow \left(\frac{\sqrt{2L}a_0}{2},\,\sqrt{L}a_1,\,\sqrt{L}a_2,\cdots, \sqrt{L}a_1,\,\sqrt{L}a_2\right)$$ (23)

ベクトルの場合の式(12)の右辺は，1を単位としたときの直角方向の成分の大きさの二乗和となっている．同様に，パーセバルの等式(21)も1を単位としたときの直角方向の成分の大きさの二乗和となっている．

以上の議論から，パーセバルの等式がピタゴラスの定理と等価であることが分かる．

3.3 ベッセルの不等式と誤差

展開する三角関数を無限大まで取らずに途中で打ち切った場合を考える．現実問題，これ はしばしば起こることである．展開の係数が解析的に計算できない場合，コンピューター を使った数値計算を行うことになる．コンピューターでは無限を取り扱うことができない ため，有限の数の三角関数で展開しなくてはならない．展開する三角関数の数を多くすれ ばより正確に元の関数を表現できるが，計算時間がさらに必要となる．そこで，展開する 関数の数と誤差の関係がわかれば，必要な展開ができる．この問題を考える．

区間$[-L,L]$で定義された関数$f(x)$を有限な数の三角関数で展開する．すなわち，

$$\bar{f}(x)=\frac{a_0}{2} +\sum_{n=1}^{k}\left[a_n\cos \frac{n\pi x}{L} +b_n\sin \frac{n\pi x}{L}\right]$$ (24)

である．この場合のパーセバルの等式は，

$$\frac{1}{L}\int_{-L}^{L}\left[f(x)\right]^2\,\mathrm{d}x \geqq\frac{a_0^2}{2}+\sum_{n=1}^{k}\left(a_n^2+b_n^2\right)$$ (25)

のような不等式になる．なぜならば，無限大まで計算するパーセバルの等式の右辺は二乗 和であるため，全ての項はゼロよりも大きい．したがって，途中までで展開を打ち切ると， 右辺は必ず左辺よりも小さくなる．式(25)をベッセルの不等式 と言う．

ここで，$k$項までのフーリエ級数の誤差の二乗の積分$E$を考える．

$$E =\dfrac{\int_{-L}^{L}\left[f(x)-\bar{f}(x)\right]^2\,\mathrm{d}x} {\int_{-L}^{L}\left[f(x)\right]^2\,\mathrm{d}x}$$

$$=\dfrac{\int_{-L}^{L}\left[\sum_{n=k+1}^{\infty}\left\{ a_n\cos \... ...\right\}\right]^2\,\mathrm{d}x} {\int_{-L}^{L}\left[f(x)\right]^2\,\mathrm{d}x}$$

$$=\dfrac{L\sum_{n=k+1}^{\infty}(a_n^2+b_n^2)} {\int_{-L}^{L}\left[f(x)\right]^2\,\mathrm{d}x}$$

$$=\dfrac{f(x)^2-L\left\{\frac{a_0^2}{2}+\sum_{n=1}^{k}(a_n^2+b_n^2)\right\}} {\int_{-L}^{L}\left[f(x)\right]^2\,\mathrm{d}x}$$ (26)

ある有限な項まででフーリエ級数の計算を打ち切った時の誤差をあたえる式である．有限 の項数でフーリエ級数を計算する場合，誤差を見積もる有用な式となる．この式の右辺は， 途中でフーリエ級数の計算を打ち切っても評価が可能な量である．
ホームページ: Yamamoto's laboratory
著者: 山本昌志