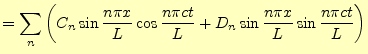2 弦の波動方程式の解(変数分離法)
2.1 偏微分方程式から連立の常微分方程式に変換
一般の偏微分方程式は解くことができないが,波動方程式のような特別な場合は解くこと ができる.通常,最初に試みる偏微分方程式の解法は変数分離法(method of separation of variables)である.これが適用できる場合,偏微分方程式は連立の常微分方程式 (ordinary differential equation)に直すことができる.波動方程式(1)--偏微分方程式のひとつ--の解は,
とそれぞれの変数の積の形に表せると仮定する.このような仮定の元で,解を計算する方 法を変数分離法という.ただし,これがいつも正しいとは限らないので注意が必要である. ここでの講義の範囲では,常に変数分離法が使えるので,諸君は安心してよい.
解の形が決まったので,元の偏微分方程式に代入する.すると,
| (3) |
が得られる.これは,
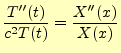 |
(4) |
となる.この左辺は時刻
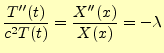 |
(5) |
となる.これを整理すると,
という連立常微分方程式になる.
ここで,![]() は実数とする.複素数と仮定しても,以降では同じような議論ができ
るが,話が複雑になるだけである.
は実数とする.複素数と仮定しても,以降では同じような議論ができ
るが,話が複雑になるだけである.
2.2 2階の常微分方程式の一般解
連立の常微分方程式(6)と(7)を解く.まずは,式 (6)からはじめる.このタイプの常微分方程式は,解を| (8) |
と仮定して,
| (9) |
がえられる.整理すると
| (10) |
となり,簡単に解ける代数方程式である.いろいろと解を改定することにより, 偏微分方程式
| (11) |
である.これから,元の微分方程式(6)の解として,次の二つのものが得ら れる.
| (12) |
いずれも,解になっている.嘘だと思うなら,それぞれの解を元の微分方程式 (6)に代入してみよ.微分方程式が成り立っていることが確認できるであろ う.元の微分方程式は線形なので,それぞれの解の和
も解である.これは元の微分方程式(6)の一般解である.なぜならば,次の ことが言え,一般解の性質を満たしているからである.
- この解には2個の未知定数が含まれている.
- さらに,元の微分方程式は2階なので,二つの未知定数を含む関数となるべきである.
ここで,教科書にならって,![]() が正の場合と負の場合について,解を分かり易く書き直
しておく.ただし,
が正の場合と負の場合について,解を分かり易く書き直
しておく.ただし,
![]() とする.また,先ほど求めた解の式(13)は複素
数まで考えている.しかし,一般に弦の振動は目に見える形なので実数の範囲に限定する
ことにする.そこで,式(13)の実数部を取り出すことにする.
とする.また,先ほど求めた解の式(13)は複素
数まで考えている.しかし,一般に弦の振動は目に見える形なので実数の範囲に限定する
ことにする.そこで,式(13)の実数部を取り出すことにする.
2.2.0.1 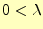 の場合
の場合
最初に| (14) |
と書き直すことができる.オイラーの公式を使っただけである.
| (15) |
ここで,
| (16) |
となる.もっと分かりやすいように書き直すと,
| (17) |
となる.これは教科書と同じ形である.
2.2.0.2 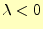 の場合
の場合
| (18) |
と式を変形する.こうすることにより,
| (19) |
となる.先ほどと同様に,実数部を解とすると,
| (20) |
が解である.これは,
![$\displaystyle X(x)= \frac{\Re(C_1)+\Re(C_2)}{2} \left[e^{-\sqrt{-\lambda}x}+e^{...
...c{\Re(C_1)-\Re(C_2)}{2} \left[e^{-\sqrt{-\lambda}x}-e^{\sqrt{-\lambda}x}\right]$](img62.png) |
(21) |
と変形できる.教科書にならってこれを記述すると,
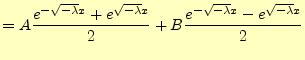 |
||
| (22) |
である.
2.2.0.3 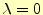 の場合
の場合
この場合は,元の微分方程式(6)から考える.それは,
| (23) |
となる.この微分方程式の一般解は,単純で
| (24) |
となる.
これまでの解の分類をまとめると
| (25) | |||||
| (26) | |||||
| (27) |
となる.
2.3 解の選定
弦の振動を示す波動方程式を変数分離した場合の空間を表す部分の微分方程式 (6)の解には3とおりある.しかし,このうちいくつかは,解として不適切で ある.弦の振動の場合,図1に示すように弦の両端で固定されている. 固定されている部分では,弦の変位| (28) |
である.この条件--境界条件--を満たすことができるのは,
| (29) |
のみである.
| (30) |
となる必要がある.これは,
すなわち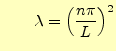 |
(31) |
である.したがって,
が解となる.
2.4 時刻の項の解
時刻の項の常微分方程式(7)は,境界条件を表す式 (31)を考慮すると,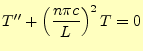 |
(33) |
となる.
となる.
2.5 弦の波動方程式の解
式(2)のように解を変数分離した場合の![$\displaystyle y_n(x,t)=B_n\sin\frac{n\pi x}{L}\left[ a_n\cos\frac{n\pi ct}{L}+b_n\sin\frac{n\pi ct}{L} \right]$](img90.png) |
(35) |
である.これは,
| (36) |
と書き直すことができる.ただし,
元の波動方程式--偏微分方程式--は線形なので,重ね合わせの原理が成り立つ.すなわ ち,解は
と書き表すことができる.これがもっとも一般的な形である.
2.6 振動のモード
弦の振動を表す波動方程式の一般解の式(37)を見ると,次のことに気 が付くであろう.- 空間的な波の形--弦の形--は,三角関数になっている.これは,
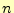 という整
数を使って,
という整
数を使って,
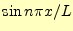 と式で表すことができる.
と式で表すことができる.
- 時間的には,三角関数で振動している.角振動数は,
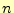 という整数を使って
という整数を使って
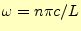 と表すことができる.
と表すことができる.
あとは,黒板に書いて説明する.
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成19年2月22日