2 有限区間で定義された関数のフーリエ級数

2.1 余弦フーリエ級数と正弦フーリエ級数

ここでは，ある区間で定義された関数をフーリエ級数で取り扱うことを考える．これまで 取り扱ってきた関数は，定義域 $[-\infty,\,\infty]$の周期関数であった．ここでは，定 義域$[0,\,L]$の有限な区間の関数を取り扱う．この範囲の外側は興味の対象外となり， その値はどうでもよい．

区間$[0,\,L]$で定義された関$f(x)$がある．このとき，$[-L,\,L]$で定義された偶関数 $F(x)$を

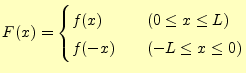$$F(x)= \begin{cases}f(x) \quad & (0\leq x \leq L)\\ f(-x) \quad & (-L\leq x \leq 0) \end{cases}$$ (1)

と定義する．これを周期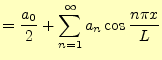$2L$の周期関数と考えるとフーリエ級数で表すことができる．す なわち，区間$[0,\,L]$で$f(x)$は

$$f(x) =\frac{a_0}{2}+a_1\cos\frac{\pi x}{L}+a_2\cos\frac{2\pi x}{L}+ a_3\cos\frac{3\pi x}{L}+\cdots$$

$$=\frac{a_0}{2}+\sum_{n=1}^\infty a_n\cos\frac{n\pi x}{L}$$ (2)

$$a_n=\frac{1}{2L}\int_0^L f(x)\cos\frac{n\pi x}{L}\,\mathrm{d}x$$

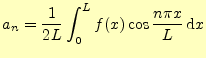と表すことができる．これを余弦フーリエ級数と言い，$[0,\,L]$では元の関数$f(x)$を正しく表して いる．区間$[0,\,L]$で関数系 $\cos n\pi x/L$は，完全直交系となっているからである． 完全直交系については，付録1を見よ．

一方，$[-L,\,L]$で定義された奇関数$G(x)$として

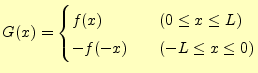$$G(x)= \begin{cases}f(x) \quad & (0\leq x \leq L)\\ -f(-x) \quad & (-L\leq x \leq 0) \end{cases}$$ (3)

を考えることもできる．$G(x)$は奇関数なので，区間$[0,\,L]$で$f(x)$は

$$f(x) =b_1\sin\frac{\pi x}{L}+b_2\sin\frac{2\pi x}{L}+ b_3\sin\frac{3\pi x}{L}+\cdots$$

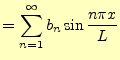$$=\sum_{n=1}^\infty b_n\sin\frac{n\pi x}{L}$$ (4)

$$b_n=\frac{1}{2L}\int_0^L f(x)\sin\frac{n\pi x}{L}\,\mathrm{d}x$$

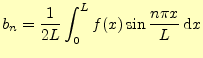と表すこともできる．これを正弦フーリエ級数と言う．

2.2 余弦フーリエ級数と正弦フーリエ級数の具体例

ここでは，余弦フーリエ級数と正弦フーリエ級数の具体例として図1のよ うに$[0,\pi]$で定義された関数を考える．

2.2.0.1 余弦フーリエ級数

余弦フーリエ級数の係数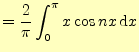$b_n$は，式 (4)から直ちに計算できる．

$$a_n =\frac{2}{\pi}\int_0^\pi x\cos nx \,\mathrm{d}x$$

$$n=0$$

$$=\pi\qquad\qquad(n=0)$$

$$n\ne 0$$

$$=\frac{2}{\pi}\left[\frac{x\sin nx}{n}\right]_0^\pi- \frac{2}{\pi}\int_0^\pi \frac{\sin nx}{n}\,\mathrm{d}x$$

$$=\frac{2}{\pi}\left[\frac{\cos nx}{n^2}\right]_0^\pi$$

$$=\frac{2}{\pi}\left[\frac{\cos n\pi-1}{n^2}\right]$$

$$n \cos n\pi=(-1)^n$$

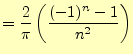$$=\frac{2}{\pi}\left(\frac{(-1)^n-1}{n^2}\right)$$ (5)

以上より，図1の余弦フーリエ級数は次のように書くことができる．

$$f(x)=\frac{\pi}{2}-\frac{4}{\pi}\left[\cos x+\frac{\cos 3x}{3^3}+ \frac{\cos 5x}{5^2}+\dots+\frac{\cos (2n-1)x}{(2n-1)^2}+\cdots\right]$$ (6)

図: 区間$[0,\,L]$で定義された関数

2.2.0.2 正弦フーリエ級数

一方，正弦フーリエ級数は，次のようになる．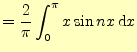

$$b_n =\frac{2}{\pi}\int_0^\pi x\sin nx \,\mathrm{d}x$$
                部分積分を使うと

$$=\frac{2}{\pi}\left[-\frac{x\cos nx}{n}\right]_0^\pi+ \frac{2}{\pi}\int_0^\pi \frac{\cos nx}{n}\,\mathrm{d}x$$

$$=\frac{2}{\pi}\left(-\frac{\pi\cos n\pi}{n}\right)+ \frac{2}{\pi}\left[\frac{\sin nx}{n^2}\right]_0^\pi$$

$$n \cos n\pi=(-1)^n$$

$$=\frac{2}{\pi}\left(-\frac{\pi(-1)^n}{n}\right)$$

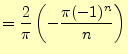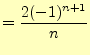$$=\frac{2(-1)^{n+1}}{n}$$ (7)

以上より，図1の正弦フーリエ級数は次のように書くことができる．

$$f(x)=2\left[\sin x-\frac{\sin 2x}{2}+\frac{\sin 3x}{3}- \dots+(-1)^{n+1}\frac{\sin nx}{n}+\cdots\right]$$ (8)

余談であるが，$x=\pi/2$の値を考えると面白い結果が得られる．f(x)での値は$\pi/2$で， 式(8)を使うと，

$$\frac{\pi}{2} =2\left[\sin\frac{\pi}{2}-\frac{\sin\pi}{2}+\frac{\sin\frac{3\pi}{2}}{3}- \dots+(-1)^{n+1}\frac{\sin\frac{n\pi}{2}}{n}+\cdots\right]$$

$$=2\left[1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+ \frac{1}{9}-\frac{1}{11}+\cdots\right]$$ (9)

が得られる．これより，ライプニッツの公式

$$\frac{\pi}{4}=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+ \frac{1}{9}-\frac{1}{11}+\cdots$$ (10)

が得られる．この式は感動的である．元々円周率は円の直径と周長の比と幾何学的にで定 義された．それが，このような単純な解析的な式で表せるのである．これで，周長と直径 を測定して円周率を求めることから開放された．

2.3 フーリエ級数とテイラー展開

区間$[0,\,L]$で定義された関数は，ここで示した余弦フーリエ級数や正弦フーリエ級数 の他に，テイラー展開(テイラー級数)で表すこともできる．ただし，フーリエ級数は不連続関数も取り扱 えるが，テイラー展開の場合連続な関数という制限はある．先ほどの例を，それぞれの級 数で展開した場合の比較を図2に示す．区間$[0,\,\pi]$では，どれも関数を正 確に記述している．しかし，区間を外れるとその振舞は大きく異なる．

どの方法がよいのだろうか?．それは，取り扱う問題に依存する．諸君は，もっとも適切 な方法を選択すれば良い．この辺の話は，来週の講義で行う．

図: 区間$[0,\,\pi]$で$f(x)=x$と定義された関数を様々な級数で表す．

ホームページ: Yamamoto's laboratory
著者: 山本昌志