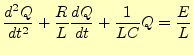2 原理
ここで述べている回路の応答の計算は,諸君が現在身につけいている数学のレベルを超えている. しかし,結果については学習の範囲内であり,直感的に理解できるであろう.従って,細 かい計算は気にしないで,結果を直感的に理解することに努めよ.ただ,結果のみを書い たのでは原理を示したことにならないので,退屈であるが正確な記述を示す.2.1 CR回路
図1に示すCR回路の過渡応答を考える.ここでは,スイッチが OFFの状態ではコンデンサーに充電されていないものとする.そして,それをONにした瞬 間から電流が流れ,コンデンサーが充電される.その充電電圧が上がり,電源電圧と等し くなると電流は流れなくなり,回路は定常状態におさまる.スイッチをONにして,定常状 態におさまるまでを過渡状態と言う.電流や電圧,あるいはコンデンサーの片側の電極の電荷量は,時間とともに変化する.そ の変化を表す式を考える.スイッチSをONにした場合,この回路の電圧に関係するキルヒ ホッフの法則は
となる.電荷
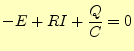 と電流は,
と電流は,
| (2) |
となる.ここで,電荷
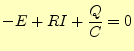 のみが時間の関数で,残りは定数である.この常微分方程式の
一般解1は,
のみが時間の関数で,残りは定数である.この常微分方程式の
一般解1は,
である.ここで,
任意常数は初期条件より決めることができる.スイッチSをONにした瞬間を
![]() として,そのときの回路の状態を初期条件と言う.ここでの初期条件は,
として,そのときの回路の状態を初期条件と言う.ここでの初期条件は,
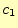 の時,コンデンサーの電荷は
の時,コンデンサーの電荷は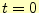
| (4) |
となる.
電荷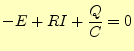 の変化が分かったので,回路の電圧や電流を求めることは簡単である.まずは,
コンデンサーの電圧は,
の変化が分かったので,回路の電圧や電流を求めることは簡単である.まずは,
コンデンサーの電圧は,![]() から簡単に求められ,
から簡単に求められ,
| (5) |
である.
| (6) |
となる.
 となる.
となる.
ここで,![]() を時定数と言い,それはコンデンサーの電圧が定常状態の63.2%になる時
間を表している.
を時定数と言い,それはコンデンサーの電圧が定常状態の63.2%になる時
間を表している.
2.2 LR回路
先ほどと同様な手法を用いて,図2のLR回路を解析する.これ を解析する前に,定性的にその応答を述べておく.スイッチSをONにした瞬間,コイルの 抵抗は無限大になる.もし無限大にならないと,有限の電流がながれそのときの電流の 変化は無限大となる.すると無限大の抵抗となり,電流はゼロにならなくては成らない. これは矛盾である.従って,ONにした瞬間の電流はゼロで,しばらくすると電流が徐々に 増加する.電流が増加して行くが,定量的な解析は,キルヒホッフの法則から始める.この回路では,
| (7) |
である.CR回路の解析と同様に,この微分方程式の一般解は,
となる.ここで,初期条件(
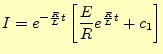 )を用いると,任意定数は
)を用いると,任意定数は| (9) |
となる.一方,抵抗の電圧は
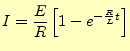 |
||
| (10) |
である.
電流や電圧が定常状態の63.2%になる時間を時定数と言い,それは![]() である.
である.
2.3 LCR回路
2.3.1 一般解
図3のLCR回路を解析する.これを定性的に理解することはな かなか難しいが,少し考えてみる.まずは,コイルがあるためスイッチを入れた瞬間の電 流はゼロで徐々に立ち上がると想像できる.途中経過は分からないが,最後にはコンデン サーが電源電圧 まで充電され,定常状態になると思われる.
まで充電され,定常状態になると思われる.
定性的に分かりにくい場合は,定量的に評価するしかない.キルヒホッフの法則から,
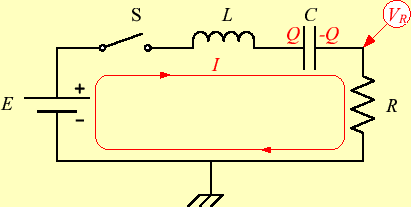 |
(11) |
が導かれる.CR回路の解析と同様に
 なので,説くべき微分方程式は
なので,説くべき微分方程式は
| (12) |
となる.付録2に示しているように,この微分方程式の解は
となる.ここで,
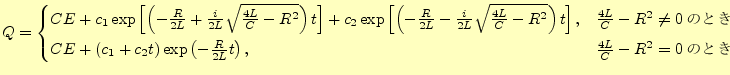 は未知定数で,初期条件によって決める.ここでは,それ
は
は未知定数で,初期条件によって決める.ここでは,それ
は
- t=0のとき,Q=0
- t=0のとき,I=0
2.3.2 減衰振動
未知定数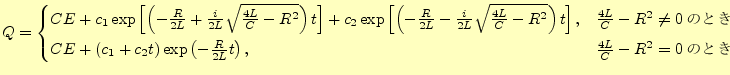 をもとめて,回路の応答を考えるが,ここでは
をもとめて,回路の応答を考えるが,ここでは
| (14) | ||
| (15) |
とする.すると,
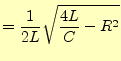 |
(16) |
である.これを微分して,電流は
となる.初期条件から,
の連立方程式が成り立つ.この連立方程式の解は,
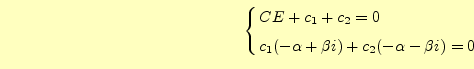 |
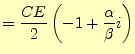 |
(19) |
となる.これを用いると,回路に流れる電流やコンデンサーの電荷の変化が分かる.ここ で,興味があるのは,図3に示されている電圧なので,それ を電流から求めることにする.回路に流れる電流
 は,この
は,この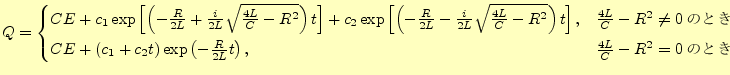 を式
(17)に代入すればよい.オイラーの公式
2を使う
と,それは,
を式
(17)に代入すればよい.オイラーの公式
2を使う
と,それは,
| (20) |
となる.これから,図3に示されている電圧は,
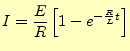 |
(21) | |
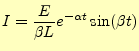 |
(22) |
となる.これは振動項
2.3.3 過減衰
次に,| (23) | ||
| (24) |
とする.後は,減衰振動の場合と全く同じように計算を進めれば良い.しかし,
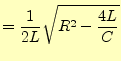 に気が付けば,減衰振動の解を利用することができる.すなわち,式
(22)の
に気が付けば,減衰振動の解を利用することができる.すなわち,式
(22)の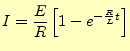 |
(25) | |
| (26) |
となる3.この場合, 振動しないで減衰する.これを過減衰と言う.
2.3.4 臨界減衰
次に,| (27) |
とする.従って,
| (28) |
である.
減衰振動の場合と全く同じように,初期条件から未知定数を決める.まずはじめに,
![]() のとき
のとき![]() の条件から,
の条件から,![]() となる.従って,
となる.従って,
| (29) |
となる.これから,電流は
| (30) |
となる.
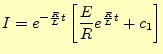 の条件から,
の条件から,
| (31) |
が得られる.これから,
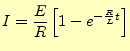 |
 |
(32) |
 |
(33) |
となる.これは臨界減衰と呼ばれる.
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成18年7月3日
![\includegraphics[keepaspectratio, scale=1.0]{figure/LCR_response/CR.eps}](img22.png)

![$\displaystyle Q=e^{-\frac{t}{CR}}\left[CEe^{\frac{t}{CR}}+c_1\right]$](img27.png)
![$\displaystyle I=e^{-\frac{R}{L}t}\left[\frac{E}{R}e^{\frac{R}{L}t}+c_1\right]$](img41.png)