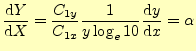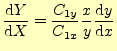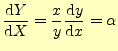2 方眼紙について

諸君が使う方眼紙は，普通の方眼紙(名前??),型対数方眼紙，両対数方眼紙が主である． これらをデータに応じて使い分ける必要がある．まず，これらの方眼紙の特徴を述べる．

2.1 普通の方眼紙

これは，もっともおなじみの，x軸とy軸ともリニアーになっているものである．説明する までもなく，よく知っているだろう．これはグラフ上の基準点からの距離($X, Y$)に，デー タ$(x,y)$を

$$X=C_{0x}+C_{1x}x Y=C_{0y}+C_{2y}y$$ (1)

のようにプロットする．$C_{1x}$と$C_{1y}$はグラフのスケールを決める定数，$C_{0x}$ と$C_{0y}$はオフセットである．難しいことを言わなくても，x軸とy軸の交点(基準点)を $(C_{0x},C_{0y})$として，等間隔に目盛りを付けていると言うだけのことである．

したがって，x軸とy軸ともリニアーになっている方眼紙では，$y=ax+b$の一次関数が

$$\frac{\mathrm{d}Y}{\mathrm{d}X} =\frac{C_{1y}}{C_{1x}}\frac{\mathrm{d}y}{\mathrm{d}x}$$

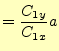$$=\frac{C_{1y}}{C_{1x}}a$$ (2)

のように，グラフ用紙で直線になる．なぜならば，$x$に依存しないで，傾きが一定となっ ているからである．このグラフの傾き $\mathrm{d}Y/\mathrm{d}X$と，スケールの比$C_2/C_1$から，デー タの1次関数の係数$a$が分かるのである．

2.2 片対数方眼紙

この方眼紙の軸は，ちょっと変わっていて，片方はリニアーで，もう一方は対数軸となっている．横軸，縦軸のいずれも対数軸にすることができる．ここでは話を簡単にするために，縦軸を対 数軸とする．そうすると，横軸はリニアー軸になる．先ほどと同様にグラフ上の基準点か らの距離を$(X,Y)$とする．この場合は，

$$X=C_{0x}+C_{1x}x Y=C_{0y}+C_{1y}\log_{10}y$$ (3)

となる．ここで，$C_{0x}$と$C_{0y}$はグラフの原点を決めるオフセット値である．$C_{1x}$と$C_{1y}$はグラフのスケールを決める定数である．

このようなグラフで直線となる関数を考えることにする．そのために，値$(x,y)$がちょっとだけ変化した場合，グラフ上の点の動きを調べてみよう．それは，

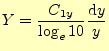$$\mathrm{d}X=C_{1x}\mathrm{d}x Y=\frac{C_{1y}}{\log_e 10}\frac{\mathrm{d}y}{y}$$ (4)

となる．これから，グラフ上で，傾き$\alpha$を持つ直線は，

$$\frac{\mathrm{d}Y}{\mathrm{d}X}=\frac{C_{1y}}{C_{1x}}\frac{1}{y\log_e 10}\frac{\mathrm{d}y}{\mathrm{d}x}=\alpha$$ (5)

となる．ここで，縦軸と横軸のスケールの比 $C_{1y}/C_{1x}$は1にしたグラフが多い²．そこで，この比を1として，話を進める．グラフ上で直線になる関数は，式13の微分方程式の解である．この微分方程式は

$$\frac{\mathrm{d}y}{\mathrm{d}x}=(\alpha\log_e 10)y$$ (6)

と見覚えがあるものに書き換えることができる．この方程式の解は，

$$y =ke^{(\alpha\log_e 10)x}$$ (7)

$$=k\times 10^{\alpha x}$$ (8)

となる．ここで，$k$は積分定数である．この結果から，方対数グラフ上では指数関数が直線で表されるのである．いうまでもないが，

$$k\times 10^{\alpha x}=k\times\exp\left(\frac{\alpha}{\log_{10}e}x\right)$$ (9)

となるので，底が10であろうが，ネピア$e$であろうが，その他なんでも指数関数が直線で表せる．

ようするに方対数グラフの傾き$\alpha$が，指数関数 $10^{\alpha x}$となるのである．

2.3 両対数方眼紙

両対数グラフは，片対数方眼紙と同じように考えることができ，データ$(x,y)$は，グラフ 上の$(X,Y)$

$$X=C_{0x}+C_{1x}\log_{10}x Y=C_{0y}+C_{1y}\log_{10}y$$ (10)

に変換される．

先ほどと同様にグラフ上で直線となる関数を考えることにする．値$(x,y)$がちょっとだけ変化した場合，グラフ上の点の動きは，

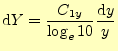$$\mathrm{d}X=\frac{C_{1x}}{\log_e 10}\frac{\mathrm{d}x}{x} \mathrm{d}Y=\frac{C_{1y}}{\log_e 10}\frac{\mathrm{d}y}{y}$$ (11)

である．これから，グラフ上で，傾き$\alpha$を持つ直線は，

$$\frac{\mathrm{d}Y}{\mathrm{d}X}= \frac{C_{1y}}{C_{1x}}\frac{x}{y}\frac{\mathrm{d}y}{\mathrm{d}x}$$ (12)

となる．両対数グラフでは，縦軸と横軸のスケールの比 $C_{1y}/C_{1x}$は1にする．

グラフ上で，傾き$\alpha$を持つ直線は，

$$\frac{\mathrm{d}Y}{\mathrm{d}X}= \frac{x}{y}\frac{\mathrm{d}y}{\mathrm{d}x}=\alpha$$ (13)

となる．この微分方程式の解は，

$$y=kx^{\alpha}$$ (14)

である．従って，両対数グラフにプロットして，それが直線であれば，$x^\alpha$の関数系であることが分かる．そして，グラフの傾きにより，$\alpha$を求めることあできる．
ホームページ: Yamamoto's laboratory
著者: 山本昌志