2 ツリーの概要
2.1 ツリーの例
ツリー(three:木)と呼ばれるデータ構造は,階層構造を持ったデータの集まりを表すのに 都合が良い.たとえば,組織図(図3),コンピューターのファイルシステムなどである.情報科 学では,データベースの中のデータの表現やコンパイラーでの原始プログラムの文法構造 などでも使われる.このように階層構造をもつデータの集まりは,これまで学習してきたデータ構造--配列 やリスト,スタック,キュー--で表すことは困難である.できないことはないが,プロ グラムが非常にわかりにくくなる.今後,諸君は階層構造を持つデータを取り扱う場合に は,ツリーを用いよ! プログラムの内容が非常に分かりやすくなる.
2.2 ツリーの基本
2.2.1 基本用語
ツリー構造にはいろいろ名称があり,それを表1と図 4に示す.なぜ,図1のようなデータ構造をツリー 構造と呼ぶか?.それは,この図を反対にしてみるのである.すると,根が一番下にきて, 枝や葉が上にあることが分かるであろう.まさに,木である.
|
|
2.2.2 特徴
子は一つの親を持つことがツリーの特徴である.二つの親を持ってはならないのである. そのため,任意の二つのノードあるいはリーフのつながりを表すパスは,一意に決まる.2.2.3 データの順序
リーフあるいはノードにはデータが格納され,それらを順序づけることができる.順序づ けの方法はいろいろあるが,次の3通りが重要である.- 先行順(preorder)
- 親のノード
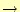 子の順に並べる.図
5のようなツリー構造では次のような並びになる.
子の順に並べる.図
5のようなツリー構造では次のような並びになる.
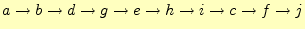
となる. - 中央順(postorder)
- 子
 親のノード
親のノード
 子の順に並べる.
これは,後で述べる2分木の他ではあまり使われない.2分木の場合,左の子
子の順に並べる.
これは,後で述べる2分木の他ではあまり使われない.2分木の場合,左の子
 親のノード
親のノード
 右の子のように順序づけることがで
きる.図5のようなツリー構造では次のような並びになる.
右の子のように順序づけることがで
きる.図5のようなツリー構造では次のような並びになる.

- 後行順(inorder)
- 親のノード
 子の順に並べる.図
5のようなツリー構造では次のような並びになる.
子の順に並べる.図
5のようなツリー構造では次のような並びになる.

このなかで,2分木に使われることの多い中央順がもっとも重要である.
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成19年7月26日
![\includegraphics[keepaspectratio,scale=1.0]{figure/ANCT_organization.eps}](img3.png)
![\includegraphics[keepaspectratio,scale=0.8]{figure/tree_peace_name.eps}](img4.png)
![\includegraphics[keepaspectratio,scale=1.0]{figure/tree_traversal.eps}](img14.png)