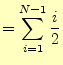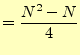単純挿入ソートは,経験を積んだトランプ師がカードを並び替えるときに使う方法である
[1].まず,2枚目をカードを取り出し1枚目と順序関係が正しい場所に入れる.次
に3枚目のカードを取り出して,1〜2枚目のカードの正しい位置に置く.これを繰り返し,
最後には52枚目のカードを取り出し,1〜51枚目のカードの正しい位置に置く.この51回
の繰り返しにより,すべてのカードを正しく並べることができる.このトランプ師の整列
の方法をコンピュータープログラムで行うのである.
単純挿入ソートは,a[0]からa[i-1]まで並び替えが終わって
いるとき,a[i]を正しい位置に入れる--ことを繰り返す方法である.その様子を図
2に示す.処理の手順は次の通りである.
- 処理するa[i]の値35よりも,48は大きいので35の場所へ移動させる.
- 次の44も35より大きいので,48の場所へ移動させる.
- 次の41も35より大きいので,44の場所へ移動させる.
- 次の39も35より大きいので,41の場所へ移動させる.
- 次の32は35より小さいので,それは移動させない.そして,元の35を39の場所へ
移動させる.
図 2:
単純挿入ソートの基本操作.a[i]を正しい位置に入れる.
|
|
単純挿入ソートの実際のプログラム(関数)は,教科書 [2]p.219のリスト
6.20のように書く.整列させる整数のデータは,配列はarray[]に格納されている.
データの個数はnumに格納されている.したがって,整列すべき整数のデータは,配
列のarray[0]〜array[num-1]に格納されている.
この関数がソートする様子を図3に示す.先に示したアルゴリズ
ムの通りであることが分かるだろう.
この関数を呼び出すときには,次のようにする.
insertion_sort(a,10);
整列すべき整数は,a[0]〜a[9]に入っている.データの個数は10個である.
図 3:
単純挿入ソートを使った整数の整列.教科書 [2]p.219のリスト
6.20 insertion_sort()関数の動作.
|
|
単純挿入ソートの計算量は,内側の繰り返し分のループ回数で決まる.教科書 [2]p.219のリスト
6.20では,jの部分のループ回数である.ここでは,その計算量のオーダーを見積も
る.
ソートするデータの個数を とする.外側のループは
とする.外側のループは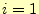 〜
〜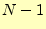 までである.データがランダムの場合,
内側のループは平均して
までである.データがランダムの場合,
内側のループは平均して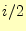 回繰り返される.したがって,内側のループの総繰り返し回数は,
回繰り返される.したがって,内側のループの総繰り返し回数は,
となる.データの個数が大きくなると, が支配的になる.したがって,計算量のオー
ダーは
が支配的になる.したがって,計算量のオー
ダーは となる.コンピューターでの処理の時間は,データ数の二乗(
となる.コンピューターでの処理の時間は,データ数の二乗(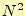 )で増
加するということである.教科書 [2]p.220の表6.3のランダムに並んでい
る配列の場合,要素数の二乗に比例して実行時間がかかっていることが分かるであろう.
)で増
加するということである.教科書 [2]p.220の表6.3のランダムに並んでい
る配列の場合,要素数の二乗に比例して実行時間がかかっていることが分かるであろう.
ホームページ: Yamamoto's laboratory
著者: 山本昌志
Yamamoto Masashi
平成19年7月26日
![]() とする.外側のループは
とする.外側のループは![]() 〜
〜![]() までである.データがランダムの場合,
内側のループは平均して
までである.データがランダムの場合,
内側のループは平均して![]() 回繰り返される.したがって,内側のループの総繰り返し回数は,
回繰り返される.したがって,内側のループの総繰り返し回数は,