シェルソートは,は1959年にD.L.Shellが考案した方法で,単純挿入ソートを改良したもの
となっている2.単純挿入ソートは,小さな値が右の方にあると,かなりの計算
量を要して,左に移動する.隣同士ひとつずつ比較を行うので,多くの計算が必要となる.
最初は大きな歩幅で,そしてだんだん歩幅を小さくしていけば,遠く離れても早く移動で
きるだろう.このような方法がシェルソートである.
単純挿入ソートは隣同士を比較したが,Shellソートでは,大きな歩幅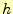 で比較する.ソートに時間のかかる大ききな数や小さな数は,一気に右や左に移動
することができる.
で比較する.ソートに時間のかかる大ききな数や小さな数は,一気に右や左に移動
することができる.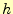 飛ばしで比較すると,
飛ばしで比較すると,
と並び替える.この並び替えには単純挿入法をつかう.
そうして,歩幅 をどんどん小さく,最後は
をどんどん小さく,最後は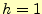 にすると並び替えは完了となる.この
にすると並び替えは完了となる.この
 の選び方にこつがあって,
の選び方にこつがあって,
 とする.式で表すと,
とする.式で表すと,
である.これは,互いに素に近い数列である.このようにすると効率が良い.最初に実行
する一番大きな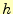 は,データの個数
は,データの個数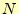 以下にしなくてはならない.教科書では
以下にしなくてはならない.教科書では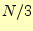 以
下にしている.他の文献 [1] [3]では,
以
下にしている.他の文献 [1] [3]では,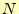 以下にしている.私だと
以下にしている.私だと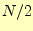 以下にするだろう.
以下にするだろう.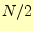 以下にすると,必ずすべてのデー
タが一度はソートされることになる.いずれにしても,計算量にあまり大差はないであろう.
以下にすると,必ずすべてのデー
タが一度はソートされることになる.いずれにしても,計算量にあまり大差はないであろう.
まとめると,シェルソートの手順は,次の通りである.
- [ステップ1] 最初の歩幅
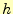 を決める.データの個数の半分以下で最大の
を決める.データの個数の半分以下で最大の
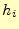 を最初の歩幅とする.
を最初の歩幅とする.
- [ステップ2]
 に対して,
a[i],a[h+i],a[2*h+i],a[3*h+i],
に対して,
a[i],a[h+i],a[2*h+i],a[3*h+i], を並び替える.これには単純挿入
ソートを使う.
を並び替える.これには単純挿入
ソートを使う.
- [ステップ2] 次のh=(h-1)/3にして,再度[ステップ2]の並び替えを実
行する.実際には,h=h/3で良い.
単純挿入ソートの実際のプログラム(関数)は,教科書 [2]p.223のリスト
6.21のように書く.整列させる整数のデータは,配列はarray[]に格納されている.
データの個数はnumに格納されている.したがって,整列すべき整数のデータは,配
列のarray[0]〜array[num-1]に格納されている.
この関数がソートする様子を図4に示す.先に示したアルゴリズ
ムの通りであることが分かるだろう.
図 4:
シェルソートを使った整数の整列.リストのプログラムのソート方
法.
|
|
シェルソートの計算量を見積もるのは,非常に難しい.移動の歩幅hに大きく依存す
るからである.式(2)のように を選べば,平均して
を選べば,平均して
 とな
ることが実験的に知られている [3].
とな
ることが実験的に知られている [3].
これは,かなり良いアルゴリズムである.後で述べるクイックソートと比較してもそんな
に悪くはない.
ホームページ: Yamamoto's laboratory
著者: 山本昌志
Yamamoto Masashi
平成19年7月26日
![]() で比較する.ソートに時間のかかる大ききな数や小さな数は,一気に右や左に移動
することができる.
で比較する.ソートに時間のかかる大ききな数や小さな数は,一気に右や左に移動
することができる.![]() 飛ばしで比較すると,
飛ばしで比較すると,
![\begin{equation*}\begin{aligned}&a[0] \leqq a[h] \leqq a[2*h] \leqq a[3*h] \leqq...
... a[4*h-1] \leqq a[5*h-1] \leqq a[6*h-1]\cdots \\ %
\end{aligned}\end{equation*}](img16.png)
![]() をどんどん小さく,最後は
をどんどん小さく,最後は![]() にすると並び替えは完了となる.この
にすると並び替えは完了となる.この
![]() の選び方にこつがあって,
の選び方にこつがあって,
![]() とする.式で表すと,
とする.式で表すと,