5 クイックソート

5.1 アルゴリズム

クイックソートのアルゴリズムは分割統治法の良い例である．分割統治法では，はじめに 問題をいくつかの部分に分けて，それを解く．そして，解いた結果を組み合わせることに より，全体の問題の解とする方法である．部分問題も全体問題も全く同じアルゴリズムが 使えるときに有効な方法である．そのような場合，再帰処理が使える．

クイックソートでは，まず適当な基準となる値を決める．そして，それより大きな値と小 さな値の数列に分割する．それぞれ分割した数列で，また同じように，基準を設けて数列 を分ける．これを繰り返すことにより，数列を整列させることができる．

後の説明は，教科書の通り．

5.2 プログラム

クイックソートの実際のプログラム(関数)は，教科書 [2]pp.226-227のリスト 6.22のように書く．整列させる整数のデータは，配列はarray[]に格納されている． データの個数はnumに格納されている．したがって，整列すべき整数のデータは，配 列のarray[0]〜array[num-1]に格納されている．

この関数がソートする様子を図5に示す．先に示したアルゴリズ ムの通りであることが分かるだろう．

図 5: クイックソートを使った整数の整列．教科書p.226-227のリスト6.22の関数のソート方 法．

5.3 計算量

クイックソートの計算量は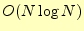， $O(N\log N)$である．大きな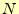$N$に対しても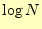，$\log N$はな かなか大きくならない．そのため，大量のデータをソートするときには，クイックソート は有利である．

ホームページ: Yamamoto's laboratory
著者: 山本昌志