2 データ構造

リストとスタック，キュー，ツリーの4つのデータ構造を学習した．

2.1 リスト

2.1.1 配列とリストの違い

順序づけられたデータを格納するという点で，配列とリストはよく似ている．しかし，使 い方やメモリーへの格納の仕方は，大きく異なるのでその違いを理解しておく必要がある．

例えば，次のような数列があるとする．

$$2,\,63,\,43,\,12,\,24,\,77,\,5,\,23,\,18,\,37,\,81,\,57,\,29,\,62,\,49,\,30$$

この数列には，個々の値とともに，その並び方にも意味がある．ようするに値とその順序 の情報を持つ．この順序づけられたデータをコンピュータープログラムで取り扱う場合，配列あ るいはリストと呼ばれるデータ構造を使う²．先ほどの例では，要素の数が多く，図で表すのが不適切なので， 次の数列

$$63,\,27,\,82,\,79,\,12$$

を使い，配列とリストの違いを説明する．

配列のモデルとメモリーへの格納の様子は，図 1のようになる．その特徴は，次の通りである．

• 配列の添字を使って，順序を表している．
• メモリーの連続した領域に，データの順序通りに格納される．

図 1: 配列のモデルとメモリーの様子．

それに対して，リストは図2のように表現することができる．その特徴は， 次の通りである．

• ポインターを使って，順序を表している．
• メモリーの連続した領域にデータを格納する必要がない．また，データの順序通 りに値を格納する必要もない．

図 2: リストのモデルとメモリーの様子．

2.1.2 リストへのデータの挿入

配列とリストにデータを挿入する場合を考える．先ほど示した数列の63の次に99を挿入す ることを考える．

配列の場合，図3のようにしてデータを挿入する．後ろの方からひ とつずつ，右側に値をコピーする．そして，データを挿入する場所にあった値のコピー が終われば，そこに挿入する値をコピーする．

データ数を$N$とすると，配列にデータを挿入する場合の処理(コピー)の回数は，平均し て$N/2$程度である．もちろん，コピー回数は挿入する場所にも依存するが，ここではあ くまで平均を問題とする．したがって，平均の処理の時間はデータ数$N$に比例し，それ を$O(N)$と表す³．

図 3: 配列のデータの挿入の様子．

それに対して，リストの場合は図4のようにしてデータを挿入する． データ63のポインターを99に接続し，データ99のポインターを27に接続する．この方法だ と，データがいくらあっても処理の回数は同じである．$O(1)$である．

配列とリストではデータを挿入する場合，処理の回数が決定的に異なる．リストの方が処 理の回数が少ない．処理の回数が異なるのは，データのメモリーへの格納の仕方による． 配列は頑固に，データと同じ並びで連続した領域に，値を格納する．一方，リストはメモ リーに適当に格納して，順序を表すポインターを使う．

図 4: リストのデータの挿入の様子．

2.1.3 リストのデータの削除

次に，先ほど99を挿入した数列

$$63,\,99,\,27,\,82,\,79,\,12$$

から，99を削除することを考える．データの削除も挿入とほとんど同じ考え方ができる．

配列の場合，図5に示した方法で，データを削除する．挿入とは逆に， 前の方から順番にコピーを繰り返す．処理の回数は$N$に比例するので，計算量のオーダーは$O(N)$となる．

図 5: 配列のデータの削除の様子．

リストの場合，図6に示した方法で，データを削除する．データ63のポ インターをデータ27に接続して，データ99を削除する．データ数とは関係なく処理の回数 は決まっており，オーダーは$O(1)$となる．

図 6: リストのデータの削除の様子．

2.1.4 データへのアクセス

次に，データのアクセスを考える．図1や2のように，配列 やリストを用いて，数列

$$63,\,27,\,82,\,79,\,12$$

がメモリーに格納されているとする．これの79というデータにアクセスするにはどうする か?

配列の場合，a[3]とすれば79のデータにアクセスすることができる．メモリーのア ドレスの順にデータが並んでいるので，「先頭のアドレス+3$\times$(ひとつのデータのバ イト数)」の計算により，目的のデータのアドレスは即座に計算できる．なんの迷いも無 く目的のメモリーアドレスが分かるので，計算量は$O(1)$となる．データがいくら増えて もデータのアクセスの時間は変化しない．

リストの場合，目的のデータへのアクセスは手間がかかる．データのある場所が分かるの は先頭のデータのみである．先頭のデータ63の次のデータ $\rightarrow$27の次のデータ $\rightarrow$82 の次のデータ $\rightarrow$79--というように先頭からたぐりよせなく てはならない．したがって，$N$個のデータがある場合，処理の平均的な回数 は$N/2$となる．計算量は$O(N)$である．データの数に比例して，処理の時間がかかるこ とを表している．

2.1.5 リストと配列の違いのまとめ

配列は目的のデータにランダムアクセスが可能で，目的のデータの値を得たり，データの 値の変更が高速にできる．添え字を指定するだけで，それらが可能である．しかし，デー タの削除と挿入には計算回数が多くなる．

一方，リストは目的のデータにアクセスするためには，シーケンシャルアクセス ⁴を行う． そのため，データへのアクセス回数が多くなり配列より低速になる．しかし，データの削 除と挿入は簡単は高速である．

また，データの個数の柔軟性はリストの方が高い．配列の場合，要素の数はコンパイル時 に予め指定する必要がある．連続したメモリー領域を確保するためである．配列の場合， データ数が予め分からない場合は，十分大きなメモリー領域を確保することになる．その ため，メモリーを無駄遣いすることがある．それに対して，リストはデータの個数は後で 追加/削除できる．

これらの違いをまとめると，表1のようになる．一般的には， データの追加/削除が多い場合にはリスト，データのアクセスが多い場合には配列を使う．

表 1: 配列とリストとの違い

	配列	リスト
データへのアクセス	添え字によるランダムアクセス可能	リストを順にたどる
アクセスのための計算量	$O(1)$	$O(N)$
データの挿入/削除	計算コスト大($O(N)$)	計算コスト小($O(1)$)
メモリーのコスト	小	配列より大
データ数	コンパイル時に決定	追加/削除可能

2.2 スタック

最後に入れたデータをはじめに取り出すスタックと呼ばれるデータ構造について説明する．

2.2.1 スタックの概要

スタック(stack)とは，最後に入れたデータを最初に取り出せるようにしたデータ構造で ある．図7のようなデータ構造である．

データ構造であるから，データを蓄えることと，それを取り出すことができる．ス タックの特徴は，最後に入れたデータが一番最初に取り出すことにある．取り出され るデータは，格納されている最新のデータで，最後に入れられたものが最初に取り出され ることから，LIFO(last in first out, 後入れ先出し)と呼ばれる．スタックの途中のデー タを取り出すことは許されない．

スタックにデータを積むこと--データの格納--をプッシュ(push)と，スタックからデー タを取り出すことをポップ(pup)と呼ぶ．

図 7: スタック

スタックは単純なデータ構造であるが，有用でいろいろな場面で使われる．例えば，次の ような場合である．

• 関数を呼び出した場合，呼び出し元のデータをいったん保存するときのデータ構 造として使われる．
• 算術式の評価(教科書 [1]のpp.189-192)．これは逆ポーランド記 法でかかれた数式を計算するプログラムである．

2.2.2 逆ポーランド記法

リストを使った応用として，逆ポーランド記法がある．コンパイラーの設計の時にこれが 役に立つ--らしい．これは，逆ポーランド記法の計算式の文字列

があるとすると，次のような順序で計算を行う．

[手順1]式を書いた文字列を取り出す．取り出す順序は式の左側から．

• 取り出した文字列が数字ならば，スタックにその数値を push する．
• 演算子(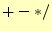$+-*/$)ならば，push を2回繰り返して，スタックから2つ数値を 取り出す．そして，演算を行う．演算結果は，スタックに push する．

[手順2]式の次の文字列について，[手順1]を行う．式の文字列がなくなる まで，これを繰り返す．

[手順3]式の文字列がなくなったとき，スタックに残った値が計算結果とな る．

具体的な計算例を，図8に示す．この例をしっかり理解する必要 がある．

二項演算子のうち，計算の順序の交換ができない場合-- - / のとき--は演算の 順序に注意する必要がある．たとえば， 5 3 - は，2なのか? -2なのか?と言う ことである．これはどちらでもよく，試験で出題する場合は，定義を示す．例えば， 「x y - はxからyを引く」と記述する．

図: 逆ポーランド記法で記述された数式 8 4 + 9 6 - / の計算の様子

2.3 キュー

最初に入れたデータをはじめに取り出すキューと呼ばれるデータ構造について説明する．

2.3.1 イメージ

キュー(queue)は，待ち行列とも呼ばれるでーた構造である．これは，窓口に並ぶ順番待ちの行列の意味で，図9のようなデータ構造となっている． スタックではデータの挿入と取り出しが列の一方からのみであったの対して，キューは列 の両端から行う．一方がデータの追加で一方がデータの取り出しとして使われる．キュー では，最初に入れたデータが一番最初に取り出されることにある．取り出され るデータは格納されている最古のデータで，最初に入れられたものが最初に取り出され ることから，FIFO(first in first out, 先入れ先出し)と呼ばれる．スタック同様，スタッ クの途中のデータを取り出すことは許されないのである．

図 9: キュー

キューはスタックに比べて少しばかり，構造が複雑になっている．実際，それを直線的な イメージのメモリーにデータを追加しようとすると，以下のような問題が生じる．

• FIFOを続けると，いずれはメモリーの端に到達して，データの追加が出来なくな る．
• データを追加したり取り出したりする毎に，データの列を移動させることも考え られる．こうすると計算量が増加して不経済である．

これを防ぐために，図10のようなリングバッファと言うものが考えられた．

図 10: リングバッファー

これは，入れられた順序通りに処理すべきデータに使われる．たとえば，次のような応用 がある．

• データをバッファーにためて，処理を行う場合．プリンターの処理などである． プリント待ちのデータをプリントキューと言うことがある．
• オンライントランザクション処理⁵の管理に用いれれる．この処理では，原則的に は到着順に処理しなくてはならない．

2.4 ツリー

2.4.1 ツリーの例

ツリー(three:木)と呼ばれるデータ構造は，階層構造を持ったデータの集まりを表すのに 都合が良い．たとえば，組織図，コンピューターのファイルシステムなどである．情報科 学では，データベースの中のデータの表現やコンパイラーでの原始プログラムの文法構造 などでも使われる．

2.4.2 ツリーの基本

2.4.2.1 基本用語

ツリー構造にはいろいろ名称があり，それを表2と図 11に示す．この図を反対にして見ると，根が一番下になり 枝や葉が上にあることが分かるであろう．まさに，木(tree)である．

図 11: ツリー構造と名称．BとEは親子関係のの例である．

図: ツリー構造の名称

構成要素	内容
ルート(root:根)	最上位のノード
ノード(node:節)	枝が分かれるところ
リーフ(leaf:葉)	子がないノード
ブランチ(branch:枝)	親と子を結ぶ線
親(parent)	上のノード
子(child)	下のノード
兄弟(brother)	同じ親を持つノード

2.4.2.2 特徴

子は一つの親を持つことがツリーの特徴である．二つの親を持ってはならないのである． そのため，任意の二つのノードあるいはリーフのつながりを表すパスは，一意に決まる．

2.4.3 2分探索木

2分木(binary tree)は，各ノードの子の数がたかだか2であるようなツリーである．これ は単純ではあるが，

• 左側の子は，その親より必ず小さい．
• 右側に子は，その親より必ず大きい．

のようにすると，順序木を作ることができる．特に2分木の順序木を2分探索木という．図12にその例を示す．2分木を，中央順(postorder)⁶に並べると，

$$11\rightarrow 15\rightarrow 20\rightarrow 23\rightarrow 31\righta... ...tarrow 55\rightarrow 65\rightarrow 73\rightarrow 81\rightarrow 88\rightarrow 94$$

となる．昇順にデータが並んでいることが分かる．

この2分探索木は応用範囲がとても広い．ツリー構造の中でもっとも単純ではあるが，アルゴリズ ムで使用される頻度はもっとも高い．単純なものほど応用範囲が広い--という一つの例 である．

この構造のあるノードの左側と右側はそれぞれの子を頂点とする同じ性質を持った木構造になる．この子孫 に対しても，同じ規準が適用されれるので，再帰による処理が可能となる．

図 12: ツリー構造(2分探索木)

2.4.4 データの作成

以下の順序で2分探索木のデータの作成の手順は以下の通りである．

• 最初のデータ--データが無いとき--は，ルートにデータをおく．
• データがある場合には，ルートから大小関係をたどり，データがまだない子孫の場所へデータを置く．

以下の順序でデータでデータが送られてきた場合，2分探索木の作成例を示す．

6,10,2,8,12,4

図13の順序で2分探索木ができる．

図 13: ツリーのノードの作成順序

手順1	手順2	手順3
手順4	手順5	手順6

2.4.5 データの追加

先ほど作成したツリーにデータ9を追加する．これも，ルートから大小関係をたどってい き，子が無いところへデータを挿入する．すると，図14のようになる．

図 14: ツリーへのデータの追加

2.4.6 データの削除

元のツリー図15からデータを削除することを考える．

図 15: データを削除する前の2分木

データを削除する場合，子が無い場合，子がひとつの場合，子がふたつの場合にに分けて 考えなくてはならない．

• 削除するデータに子が無い場合は，そのまま削除する(図16)．
• 削除するデータがひとつの子をもつ場合は，削除した場所にその子と子孫を入れ る(図17)．
• 削除するデータがふたつの子を持つ場合．削除した場所に，左側の子孫の最大値 (あるいは右側の子孫の最少値)を移動させる(図18)．

図 16: 元のツリー図15から3を削除．子が無い場合は，そのまま削除す る．

図 17: 元のツリー図15から2を削除．子がひとつの場合は， 削除した部分にその子を移す．

図 18: 元のツリー図15から10を削除．子が二つの場合は，削 除した部分に，左側の子孫の最大の値をもつノードを移動させる．

2.4.7 2分木の実装

2分木は，ノードとその接続状態を表すブランチからできている．C言語でこれを表現する ためには，ノードの中でデータと接続状態を表す変数を用意すればよい．リストを思い出 せ，それとほとんど同じではないか! リストと同じように，ノードをあわす構造体を使え ばよい．

	typedef struct node_tag{
	  int value;
	  struct node_tag *left;
	  struct node_tag *right;
	}node;

このようなノードを使うと，図19のようにツリー構造を表すことができる． ノードに子が無い場合には，子を表すポインターにNULLを入れる．これはヌルポイ ンターと呼ばれ，「なにも指し示さないポインター」と言うことを明示している．

ツリー全体を表すために，ルートを表す構造体

	node *root_tree=NULL;

を宣言しておく．初期値は意味のないポインター(NULL)を入れておく．最初はルートがないため， それを表すポインターは意味が無いためである．

図 19: 構造体を使ったツリー構造

ホームページ: Yamamoto's laboratory
著者: 山本昌志